Théorème de Lagrange

[Anaisdeistres]

Bonjour,

Je n'ai pas compris le théorème de Lagrange. Par exemple pour le groupe Z6,+ on peut avoir des sous-groupes d'ordre 1,2,3 et 6. Ok mais je trouve aucune explication claire et simple du raisonnement sur internet. Quelqu'un peut me faire un raisonnement sur cet exemple s'il vous plaît ?

Merci !

[Mimosa]

Bonjour

Sur cet exemple il y a effectivement des sous-groupes de tout ordre possible, ce qui n'est pas toujours vrai.
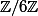Ici, tu as d'ordre 1, d'ordre 3, d'ordre 2, et d'ordre 6.

Voilà une explication simple dans le cas général. Soit un groupe d'ordre et un sous-groupe d'ordre . Pour tout 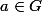on considère l'ensemble 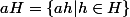. On montre d'abord que 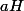a éléments. Ensuite on vérifie que


Ceci montre que les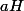 distincts forment une partition de , et comme chacun a éléments, est multiple de .

[Anaisdeistres]

Non malheureusement c'est le genre de définition que je ne comprend pas je préfererai une explication avec des mots français s'il vous plaît merci

[tournesol]

On ne peut pas faire plus simple que la méthode de mimosa .
Cependant , ce n'est pas la première fois que tu viens sur le site et je sais donc ce que tu es capable de comprendre .
Je vais donc te détailler cette méthode et tu vas comprendre .
Soit donc G , un groupe fini , et H un de ses sous groupes .
1)Pour tout a dans G , l'application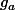 (multiplication à gauche par a) G dans G est injective .
En effet ssi ssi par régularité de a .
Conséquense : Pour toute partie A de G , A et ont le même nombre d'éléments .
Donc H et ont le même nombre d'éléments m .
2)Il suffit de montrer que G est réunion disjointe de certains
Soit x appartenant à G .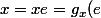 . Mais e appartient à H car H est un sous groupe de G .
Donc .Notons que x n'appartient pas seulement à .
En effet , si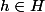 , on a et donc .
Donc x appartient à certains et donc G est réunion de certains .
En fait x ne peut appartenir qu'à un seul .
En effet , si x appartient à et à , alors il existe h et h' dans H tels que .
Soit alors y appartenant à . Alors 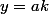avec k appartenat à H .
Mais .
De on obtient
Donc . Et comme H est un groupe , .
Donc .
On a montré que
On montre de même que
x n'appartient donc qu'à un seul même si celui ci admet plusieurs paramétrisations (par a , par a' , etc)
On a donc montré que G est réunion disjointe de certains .
Et comme tous les ont le même nombre d'éléments et que ce nombre est le cardinal m de H ,
m divise le cardinal de G .

[Anaisdeistres]

Oui merci beaucoup c'est une très belle démonstration dommage que je ne la comprend pas j'ai un peu de mal à comprendre les démonstration en générale mais j'avoue que celle-la je décroche à la deuxième ligne.

Bon par contre en français pour trouver l'ordre des sous-groupes de (Z6,+) par exemple (car on comprend toujours mieux en utilisant un exemple ?) on a comme ordre 1, 2, 3 et 6 car 6/1=6, 6/2=3, 6/3=2, 6/6=1 et on a pas 4 et 5 car 6/4 et 6/5 n'est pas un nombre entier ?

Merci

Xoxo

[Mimosa]

Pour trouver l'ordre de 4 dans calcule 4+4+4+... jusqu'à trouver 0.

[Anaisdeistres]

Ok merci

[Lostounet]

Salut,
Si je te demande de trouver le reste de la division euclidienne de 4^208 par 7 tu ferais quoi?
Tu regarderais 4^208 mod 7.

Si tu te souviens, la méthode consiste à trouver un entier n tel que 4^n=1 mod 7 pour ensuite élever les deux côtés à une grande puissance.

Donc si on est naïf on va faire 4^1 mod 7 puis 4^2 mod 7 puis ...
Jusqu'à trouver ce n.

Mais si on est malin on va uniquement regarder n=1,2,3 et 6


Tout n qui serait solution est parmi les diviseurs de 6 et ce n'est pas une coincidence.

On travaille dans le groupe (Z/7Z)* multiplicatif ie le groupe formé par les entiers modulo 7 sauf 0 (car 0 n'a pas d'inverse). Il possède 6 éléments (il est donc d'ordre 6).

Donc si on a un sous-groupe contenant 4, il sera d'ordre un diviseur de 6 par le théorème de Lagrange.

Vérifions cela sur cet exemple.
On peut construire un sous-groupe contenant 4 comme suit:
On met 1 (le neutre) et le 4 dedans
Mais 4*4=16= 2 mod 7 donc on met 2 dedans (car le produit de deux éléments d'un groupe doit rester dans ce groupe)
2*2=4 mod 7
2*4=1 mod 7
Donc la boucle est bouclée: on a construit un sous groupe {1;2;4} contenant 4. Ce groupe est d'ordre 3.
C'est un sous-groupe d'un groupe fini (Z/7Z* est cyclique) donc il est cyclique cela veut dire que 4^3=1 mod 7.



Conclusion:
4^3=1 mod 7
(4^3)^69=1^69 mod 7
4^207=1 mod 7
4^208=4 mod 7