Théorème de Lagrange

[Xavier63]

Je suis un autodidacte en maths et je me penche sur des cours de maths spé.
Quelqu'un pourrait-il me donner 3 exemples concrets de groupes fini G et de sous groupes H qui vérifie le théorème de Lagrange.
Par exemple si j'ai le groupe fini : Z/ 7Z je ne trouve pas de sous groupe
ou si je prends le groupe des inversible de Z/9Z (càd U(Z/9Z))

je vous remercie à l'avance

[L.A.]

Bonjour,

7 étant un nombre premier, Z/7Z n'a que 2 sous-groupes triviaux : {0} et Z/7Z d'ordres 1 et 7.
Le groupe U(Z/9Z) = {1,2,4,5,7,8} est un groupe cyclique d'ordre 6.
Il possède 4 sous groupes : {1}, {1,8}, {1,4,7}, {1,2,4,5,7,8} d'ordres 1, 2, 3 et 6

[Xavier63]

je te remercie

[Xavier63]

une question supplémentaire

si je prends le groupe additif (Z/4Z, +)

Z/4Z = { 0, 1, 2, 3}

les seuls sous-groupes sont {0} et { 0, 2}
(1 et 3 sont générateurs)

je ne trouve pas l'égalité avec le théorème de Lagrange !

merci

[GaBuZoMeu]

je ne trouve pas l'égalité avec le théorème de Lagrange !

Qu'est-ce que ça veut dire ?
Au fait, tu oublies le groupe tout entier parmi ses sous-groupes.

[Xavier63]

Question supplémentaire:

Pourriez-vous me donner un exemple de groupe G et d'un sous groupe H (de G) qui ne soit pas distingué ?

Je vous remercie

[GaBuZoMeu]

Tu pourrais peut-être commencer par répondre aux questions qu'on te pose ?

Que veut dire "je ne trouve pas l'égalité avec le théorème de Lagrange !" ??

Un sous-groupe non distingué ? C'est forcément dans un groupe non abélien. Un exemple minimal : le groupe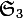 des permutations de 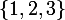qui a 6 éléments. Peux-tu en faire la liste ? Le sous-groupe à deux éléments formé de l'identité et de la transposition n'est pas distingué. Peux-tu faire la liste des conjugués de ce sous-groupe ?

[Xavier63]

Pardon de n'avoir pas répondu à ta première question. Oui le théorème de Lagrange est bien vérifié, pour résumer :

Soit le groupe additif (Z/4Z, +)

Z/4Z = { 0, 1, 2, 3}

les seuls sous-groupes sont {0}, { 0, 2} et {0, 1, 2, 3}

L'ordre des sous groupes (1, 2, 6) divise bien l'ordre du groupe (6) donc vérifie le théorème de Lagrange !

la 2e question: un sous groupe est distingué si il est abélien. Aussi soit x élément d'un groupe G, le sous groupe H est distingué si xH = Hx

S3 = { {1, 2, 3}, {2, 1, 3}, {3, 2, 1}, {1, 3, 2}, {2, 3, 1}, {3, 1, 2} }

S3= { I, T12, T13, T23, C231, C312} où I = Identité, T = transposition et C = cycle. Enfin il me semble ...!

ou bien S3= { I, T12, T13, T23, (T13 o T23), (T23 o T12)} toute combinaison supplémentaire nous fait retomber sur un élément du groupe

Je n'ai pas compris la question suivante : " Le sous-groupe à deux éléments formé de l'identité et de la transposition n'est pas distingué. Peux-tu faire la liste des conjugués de ce sous-groupe ? "

Je crois comprendre que tu demandes la composée d'une transposition et de l'identité, dans ce cas le résultat est le même : T o I = I o T
Enfin il me semble que je n'ai pas compris cette question ...!

[GaBuZoMeu]

L'ordre des sous groupes (1, 2, 6) divise bien l'ordre du groupe (6)

6=4 ???

un sous groupe est distingué si il est abélien.

Non, absolument pas.
La définition correcte est presque celle que tu donnes après. Sauf qu'elle est mal quantifiée : un sous-groupe H est distingué dans G si et seulement si, pour tout x de G, xH=Hx

Tu as presque bien fait la liste des éléments du groupe . Sauf que le cycle est le même que le cycle . Essaie de corriger ta liste.

Pour l'exemple que je t'ai donné, il s'agit de vérifier que est un sous-groupe de , et que ce n'est pas un sous-groupe distingué.

[Xavier63]

Oui par pardon, C'est 4 et non 6.

J'avais compris qu'un groupe abélien est forcément distingué ! c'est faux ?

correction : je ne vois l'erreur !
il y a bien 3! dans le groupe, donc 6 éléments :
S3 = { {1, 2, 3}, {2, 1, 3}, {3, 2, 1}, {1, 3, 2}, {2, 3, 1}, {3, 1, 2} }
S3= { I, T12, T13, T23, (T13 o T23), (T23 o T12)}

sinon
H= {Id, (1,2) }

(1, 3) H n'est pas égal à H (1,3) donc non distingué !

[GaBuZoMeu]

J'avais compris qu'un groupe abélien est forcément distingué ! c'est faux ?

J'ai l'impression que tu te mélanges les pinceaux.

Distingué, ça qualifie un sous-groupe d'un groupe ; il y a deux groupes dans l'histoire.

Soit H un sous-groupe de G. Si H est abélien, il n'a aucune raison d'être distingué dans G. L'exemple que tu viens de traiter le montre : le sous-groupe formé de l'identité et d'une transposition est abélien, et il n'est pas distingué dans .

Par contre, si G est abélien, alors tout sous-groupe H de G est distingué dans G. Peux-tu le démontrer ?

[Xavier63]

nos messages se croisent !
Je réfléchis pour démontrer : " si G est abélien, alors tout sous-groupe H de G est distingué dans G. Peux-tu le démontrer ?"

[Xavier63]

soit G un groupe abélien et H sous groupe de G. H est un sous groupe si pour tous couple (x,y) élément de H nous avons xy^-1 élément de H donc x élément de Hy. D'autre part ... !!!! je jette l'éponge

je ne sais pas démontrer la question suivante : " si G est abélien, alors tout sous-groupe H de G est distingué dans G. Peux-tu le démontrer ?"

merci de me le démontrer

[GaBuZoMeu]

Il suffit d'utiliser la définition de sous-groupe distingué (dans la version que j'ai corrigée).
Ce n'est vraiment pas difficile, je t'assure.
Que faut-il vérifier ?

[Xavier63]

je réponds à une question précédente: "Le sous-groupe à deux éléments formé de l'identité et de la transposition n'est pas distingué. Peux-tu faire la liste des conjugués de ce sous-groupe ? "

S3 = { {1, 2, 3}, {2, 1, 3}, {3, 2, 1}, {1, 3, 2}, {2, 3, 1}, {3, 1, 2} }
S3= { Id, (1,2), (1,3), (2, 3), ((2,3) o (1,2)), ((1,3) o (2,3))}

sinon
H= {Id, (1,2) }

Id H= H Id
(1,2) H = H (1,2)
(1, 3) H = { (1,3), (1,3) o (2,3)} différent de H (1, 3) = {(1,3), (2,3) o (1,2) }
(2, 3) H = { (2,3), (2,3) o (1,2)} différent de H (2, 3) = {(2,3), (1,3) o (2,3) }
((2,3) o (1,2)) H = {(2,3) o (1,2), (2,3) } différent de H ((2,3) o (1,2)) = {(2,3) o (1,2), (1,3) }
((1,3) o (2,3)) H = {(1,3) o (2,3), (2,3) } différent de H ((1,3) o (2,3)) = {(1,3) o (2,3), (1,3) }

Le sous groupe : H= {Id, (1,2) } n'est pas distingué


Je réfléchis sur : si G est abélien, alors tout sous-groupe H de G est distingué dans G. Peux-tu le démontrer ?

[Xavier63]

si un groupe G est abélien tous sous groupe H de G est aussi abélien. Donc pour tous x élément de G xH = Hx

[GaBuZoMeu]

Le fait que H soit abélien n'entraîne pas que xH=Hx pour tout x de G.
Le fait que G soit abélien, oui.