Théorème de dérivation des fonctions composées et matrice

[Fitzounet]

Bonjour,

Si je dispose de deux fonctions et et que je cherche à dériver , je peux procéder comme ceci :



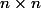
Supposons maintenant que je dispose d'une fonction à valeurs réelles où A est une matrice et les coefficients de dépendent de . Je cherche à dériver par rapport à , comment cela marche dans ce cas ? car et sont toutes les deux des matrices, donc je ne peux pas faire



Merci de vos réponses.

[arnaud32]

tu confonds derivee et differentielle

[zygomatique]

salut

il faut en dire plus sur la fonction f ...

[Fitzounet]

Merci de vos réponses. Je ne pensais pas qu'il était nécessaire d'expliciter mais allons-y :



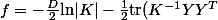où

représente le déterminant de

tr représente la trace

est une matrice fixée

avec dérivable par rapport à chaque variable

.

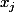
Moi j'ai envie de calculer le gradient de (vue comme fonction des ) , il faut donc évaluer les .

[zygomatique]

f c'est f(K) ? ....

qui est D ?

si f = f(K) alors ::

la trace est linéaire donc égale à sa différentielle .... mais il y a en argument K^-1 donc ...

maintenant ça me semble bien compliqué ....

[Fitzounet]

D est une constante.

[SLA]

f c'est f(K) ? ....

qui est D ?

si f = f(K) alors ::

la trace est linéaire donc égale à sa différentielle .... mais il y a en argument K^-1 donc ...

maintenant ça me semble bien compliqué ....

Salut!
Faut pas éxagérer, c'est pas si compliqué que ça: on connait les différentielles des fonctions déterminant et inverse (au pire, on trouve ça vite).
On a: et encuite, on utilise les formules sur les différentielles des composées, ainsi que les sommes des fonctions.

Cordialement