Dérivation de 3 fonctions composées

[chelsea-asm]

Bonjour,

Je dois dériver la fonction f définie par On me dit que je dois envisager deux cas. D'après la suite de l'énoncé j'en déduis que le premier cas est x positif, et le deuxième cas x nul ou négatif.

En ce qui concerne je sais que sa dérivée est
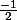
Pour le reste j'ai donc 3 fonctions :




et

Je dérive d'abord (v o u), ce qui me fait v'(u(x)) u'(x)




D'où :

Ensuite, dois-je faire une sorte de (g o f) avec g=argch et f(x) = v'(u(x)) u'(x) ?

Merci pour votre aide

[Skullkid]

La démarche est bonne, par contre tes calculs sont faux, tu as dérivée la fonction racine carrée comme s'il s'agissait de la fonction inverse.

f°g°h est la composée de deux fonctions : f et g°h, donc

[chelsea-asm]

Ah ben oui, si je commence par me tromper dans les dérivées je vais partir loin... ^^ merci !
Je vais ressayer !

[chelsea-asm]

Est-ce que cette fois-ci le calcul est juste ? :

[Skullkid]

C'est bon, y a juste le (x) qui manque après (v°u)'.

[chelsea-asm]

Bon désolé pour le triple poste, mais en appliquant :

Je trouve :

x

Ce qui me donne :



Qu'en pensez-vous ?

Merci encore

[Skullkid]

C'est correct, mais tu peux encore simplifier.

[chelsea-asm]

Je trouve :


Cela me ferait 1/2 ? Et j'obtiens une fonction dérivée constante... :S

[Skullkid]

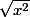
Pas exactement. n'est pas égal à x quel que soit x.

[Bony]

[chelsea-asm]

J'ai :


Si j'applique :

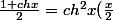Cela me permet de simplifier par ceci :



Après, je trouve que la solution que j'avais avant était plus simple...

[bentaarito]

Je trouve :


Cela me ferait 1/2 ? Et j'obtiens une fonction dérivée constante... :S

donc ta fonction est plutôt constante par intervalle

[Bony]

Au lieu de l'appliquer désespérement à ta dérivée, tu peux déjà essayer de simplifier l'écriture de base avant de dériver

[Skullkid]

chelsea-asm, l'indication de Bony sert surtout pour simplifier l'expression de la fonction de base, pas de sa dérivée.

Quelle que soit la méthode de calcul, tu arriveras à la même chose, c'est-à-dire que la dérivée de f est donnée par f'(x) = shx / (2|shx|) - 1/2 = sgn(x)/2 - 1/2 avec sgn la fonction signe (sgn(x) = x/|x|), à partir de quoi tu peux en déduire une expression simplifiée de f (si c'est le but de l'exercice). Bien sûr, avec la formule donnée par Bony, on peut trouver cette expression sans avoir à dériver.

[chelsea-asm]

Quand j'ai est-ce que c'est égal à ?
Sachant que chx est toujours positif ??

Merci

[Skullkid]

Quand j'ai sqrt{ch^2(\frac{x}{2})} est-ce que c'est égal à ch(\frac{x}{2}) ?
Sachant que chx est toujours positif ??

Merci

Oui, si a est positif alors sqrt(a²) = a.

[Bony]

En fait, Argch(ch(x)) = x si x est positif et -x si x est négatif

[dfco]

Bon désolé pour le triple poste, mais en appliquant :

Je trouve :

x

Ce qui me donne :



Qu'en pensez-vous ?

Merci encore

Tu t'es trompé c'est:
(shx/(2sqrt((1+chx)/2))*1/(chx-1)

[Anonyme]

Bonjour chelsea-asm
C'est juste pour info :
Si tu ne connais plus la dérivée de la fonction argch qui est une fonction dérivable sur ]1,+infini[ de fonction dérivée :
tu peux écrire (si tu t'en souviens) que : argch(t)=
avec dans cet exo

[chelsea-asm]

Merci beaucoup ! Mais la dérivée je m'en souvenais d'où mes calculs.
Mais j'ai trouvé que mon résultat avec pouvait me permettre de distinguer deux cas, sh positif ou négatif, et terminer l'exercice comme ça ! Merci pour toute votre aide