Théorème du changement de variable (intégrales impropres)

[shar]

Bonsoir, dans mon cours , le thrm est défini de cette façon:

Soit f une fonction continue sur ]a,b[]a,b[ et φ:]α,β→]a,b[φ:]α,β→]a,b[ bijective, strictement croissante et de classe C1 , les intégrales sont de même nature et égales en cas de convergence.


Ma question concerne les hyposthèses sur l'application phi, notamment pourquoi la bijectivité est-elle nécessaire? Dans le cours de math supp ce n'était pas nécessaire si je me souviens bien

[Kolis]

Bonjour !
"bijectif" est en fait inutile. En revanche la monotonie stricte est indispensable pour faire une composition de limites.
Et une fonction continue strictement monotone étant bijective (avec un ensemble but à préciser) !...

[Ben314]

Salut,

Soit f une fonction continue sur ]a,b[]a,b[ et φ:]α,β→]a,b[φ:]α,β→]a,b[ bijective, strictement croissante et de classe C1 , les intégrales sont de même nature et égales en cas de convergence.

Non, ni la bijectivité, ni la stricte monotonie ne sont ni l'une ni l'autre "indispensable" et normalement tu devrait parfaitement être capable de le voir tout seul en refaisant la preuve de ce résultat qui tient tout au plus 3 lignes vu les hypothèse archi gentilles que tu as (*) (donc c'est bien évidement la preuve qu'il faut comprendre et pas le résultat qu'il faut apprendre)

(*) A savoir de supposer que la fonction f est continue et pas uniquement qu'elle est Riemann-Intégrable.

[Kolis]

Bonsoir Ben314 !
Je ne vois pas comment tu composes les limites (cas des intégrales impropres) si le changement de variables fait "sortir" de l'intervalle autorisé.

On retrouve l'"emmerde" des limites épointées...

Je n'avais pas lu ta remarque mais même avec la continuité, je ne vois pas :
Soit une primitive de .
Je pense que tu veux écrire ceci :

Mais pour utiliser il faut être certain que .

[Ben314]

Je ne vois pas comment tu composes les limites (cas des intégrales impropres) si le changement de variables fait "sortir" de l'intervalle autorisé.

Si ce que tu appelle "faire sortir", c'est le fait fait que l'image par phi de l'intervalle ]alpha,beta[ n'est pas contenue dans l'intervalle ]a,b[, effectivement ça déconne, mais le fait que ça déconne n'a pas le moindre rapport avec le théorème en question (ni avec les limites épointées) : ça provient du constat complètement débile que si on a deux application complètement quelconques phi de A dans B et f de C dans D, ben pour pouvoir parler de f o phi , il faut évidement que B soit contenu dans C !!!

[Ben314]

Au départ on a une fonction continue (avec et éventuellement égaux à )
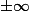
Par définition, dans ce cas là (f supposée continue) où F est une primitive quelconque de sur ]a,b[ (et évidement, on dit que l'intégrale est "convergente" lorsque les deux limites existent)

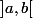
Ensuite, on prend une fonction de classe C1 qui atterrit évidement dans sinon ça aucun aucun sens de parler de (*) et on a alors vu que est une primitive de .

Bilan : pour que les deux intégrales soient "de même nature et égales si elle sont convergentes", ben il suffit d'avoir et ce qui n'impose rien en ce qui concerne le comportement de ailleurs qu'au voisinage de et de .

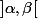
(*) Mais il faut évidement constater que, si f était était en fait définie sur un intervalle ]a',b'[ plus grand que ]a,b[, ça poserait pas le moindre problème que aille de dans ]a',b'[ et pas dans ]a,b[. Bref, cette condition que elle ne sert qu'à une et une seule chose, c'est à ce que existe.