Intégrales impropres

par **jeje56** » 12 Fév 2009, 10:19

Bonjour,

Est-il possible simplement de justifier la convergence sur R de 1/(t²+t+2) ?

Je dis :

En +oo : f(t) équivalent à 1/(t²+t) qui est majorable par 1/t² qui est intégrable...

Est-ce correct ? Comment faire en -oo ?

Après calculs, je trouve

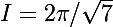
, quelqu'un peut-il confirmer ?

Merci bcp !

par **XENSECP** » 12 Fév 2009, 12:52

Hum la justification de la convergence est correcte... En gros c'est en + ou - infini qu'il faut majorer la fonction f et par comparaison aux intégrales de Riemann, tu en conclus que f est intégrable sur R !

Pour la valeur de l'intégrale bah euh attends ^^

par **girdav** » 12 Fév 2009, 12:56

Bonjour.
En

, tu peux directement dire que

~

.
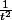
Pour

, on fait le changement de variable pour se ramener au cas précédent.
Pour la valeur, ça doit sûrement être correct (on bricole pour faire apparaître l'arctangente).

par **XENSECP** » 12 Fév 2009, 12:57

Pour la valeur, je suis d'accord aussi ;)

par **XENSECP** » 12 Fév 2009, 12:58

girdav a écrit:Bonjour.
En , tu peux directement dire que ~ .
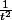
Pour , on fait le changement de variable pour se ramener au cas précédent.
Pour la valeur, ça doit sûrement être correct (on bricole pour faire apparaître l'arctangente).

Hum pas ce changement de variable ^^
Mais bon avec l'arctan oui, je pense qu'il l'a fait correctement même si le détail n'était pas passionnant ^^

Remarque : séparer l'intégrale en 0 n'est pas vraiment utile

par **jeje56** » 12 Fév 2009, 13:40

XENSECP a écrit:En gros c'est en + ou - infini qu'il faut majorer la fonction f et par comparaison aux intégrales de Riemann, tu en conclus que f est intégrable sur R !

Merci pr ta réponse et ta confirmation pr le résultat ;-)

En -oo, je ne peux pas écrire :
1/(t²+t) <= 1/t²...
Là est mon problème...

Merci !

par **Joker62** » 12 Fév 2009, 14:02

Pourquoi tu sépares en 0 ?
Et oui c'est de l'arctan on met sous forme canonique est basta :o

par **jeje56** » 12 Fév 2009, 14:09

Oui inutile c'est vrai...

par **XENSECP** » 12 Fév 2009, 14:18

jeje56 a écrit:Merci pr ta réponse et ta confirmation pr le résultat

En -oo, je ne peux pas écrire :
1/(t²+t) <= 1/t²...
Là est mon problème...

Merci !

Euh il te suffit de dire que f(t) est équivalent à 1/t² en + ou - l'infini et comme f est positive tu appliques la propriété de convergence

par **jeje56** » 12 Fév 2009, 14:24

Oui d'accord, merci à toi !

Intégrales impropres

Intégrales impropres

Qui est en ligne