Bonjour,
j'étudie actuellement les séries numériques et j'ai un petit problème, pour étudier leurs convergences il faut déterminer le terme général de chaque série or je ne sais pas quel terme choisir en fonction de la série.
Par exemple si la fonction est n^(1/n)-1 sachant que n^(1/n)=e^(ln n / n) et grâce aux développements limités on obtient:
n^(1/n)-1 = (ln n)/n + (ln n)² / 2n² + o[(ln n)² / 2n²]
D'après le cours j'obtiens que le terme général est (ln n)² / 2n² mais pourquoi ce n'est pas (ln n)/n?
Merci beaucoup
Terme général d'une série numérique
4 messages
- Page 1 sur 1
Salut,
J'ai un peu l'impression que tu t'embrouille dans le vocabulaire...
Une série, c'est un truc qui s'écrit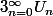 . Ce que l'on apelle le "terme général" de la série, ben c'est simplement
. Ce que l'on apelle le "terme général" de la série, ben c'est simplement 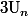 .
.
Visiblement, vu ce que tu écrit (développement limité...), ce que tu cherche, c'est un équivalent du terme général, c'est à dire un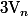 le plus simple possible tel que
le plus simple possible tel que 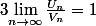 .
.
Ensuite, si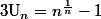 alors, y'a pas photo, un équivalent, c'est
alors, y'a pas photo, un équivalent, c'est }{n}) et pas
et pas \big)^2}{2n^2}) ...
...
J'ai un peu l'impression que tu t'embrouille dans le vocabulaire...
Une série, c'est un truc qui s'écrit
Visiblement, vu ce que tu écrit (développement limité...), ce que tu cherche, c'est un équivalent du terme général, c'est à dire un
Ensuite, si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si on procède par équivalence u_n est équivalente à 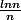 cette dernière est le terme d'une série divergente, comme on a un signe constant alors la série de terme general
cette dernière est le terme d'une série divergente, comme on a un signe constant alors la série de terme general  est bien divergente.
est bien divergente.
Si on procède par DL, là il faut quand même pousser le DL jusqu'à l'ordre 2 puisqu'on connait pas la nature de la série de terme général)
Remarque :
Lorsque le terme général d'une série numérique est de la forme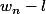 où
où  est la limite de la suite
est la limite de la suite 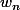 souvent on procède par équivalence si ceci ne donne pas de résultat on écrira un DL.
souvent on procède par équivalence si ceci ne donne pas de résultat on écrira un DL.
Si on procède par DL, là il faut quand même pousser le DL jusqu'à l'ordre 2 puisqu'on connait pas la nature de la série de terme général
Remarque :
Lorsque le terme général d'une série numérique est de la forme
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
