Dans la formule du crible, on rencontre la notation
Symbole sigma et inégalité d'indices
4 messages
- Page 1 sur 1
Symbole sigma et inégalité d'indices
Bonjour,
Dans la formule du crible, on rencontre la notation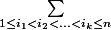 . Cela signifie si j'ai bien compris toutes les possibilités de k-uplet possibles d'ensembles que l'on peut former. Ma question est pourquoi cette notation traduit ceci, car je ne vois pas pourquoi. Merci.
. Cela signifie si j'ai bien compris toutes les possibilités de k-uplet possibles d'ensembles que l'on peut former. Ma question est pourquoi cette notation traduit ceci, car je ne vois pas pourquoi. Merci.
Dans la formule du crible, on rencontre la notation
Re: Symbole sigma et inégalité d'indices
On peut décomposer cette somme, en figeant à chaque fois la valeur de  .
.
On obtient donc :
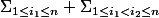 etc
etc
La première somme est simple.
La 2ème somme, pour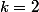 : on prend tous les couples
: on prend tous les couples ) avec
avec 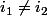 , et prenant une seule fois chaque couple (on prend le couple
, et prenant une seule fois chaque couple (on prend le couple ) , mais pas le couple
, mais pas le couple )
Puis pour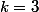 , on prend tous les triplets, une seule fois chaque triplet, etc etc.
, on prend tous les triplets, une seule fois chaque triplet, etc etc.
On obtient donc :
La première somme est simple.
La 2ème somme, pour
Puis pour
Re: Symbole sigma et inégalité d'indices
Ok merci c'est plus clair ! Mais moi je connais juste pour I et J disjoints : 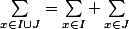 . Peut-on se ramener à des unions pour appliquer ceci, ou est-ce une autre règle ?
. Peut-on se ramener à des unions pour appliquer ceci, ou est-ce une autre règle ?
Re: Symbole sigma et inégalité d'indices
Bonjour,
Un autre point de vue, qui me semble bien adapté à la formule du crible où on considère toutes les intersection à
à  pour un certain
pour un certain  inférieur ou égal à
inférieur ou égal à  . On fait alors une somme indexée par l'ensemble des parties de
. On fait alors une somme indexée par l'ensemble des parties de 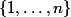 à
à  éléments. Une telle partie peut être ordonnée par l'ordre naturel sur
éléments. Une telle partie peut être ordonnée par l'ordre naturel sur 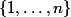 et ceci fournit une bijection entre l'ensemble des parties à
et ceci fournit une bijection entre l'ensemble des parties à  éléments de
éléments de 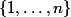 et l'ensemble des
et l'ensemble des  -uplets d'entiers
-uplets d'entiers ) tels que
tels que 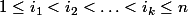 . On a ainsi (pour une mesure
. On a ainsi (pour une mesure  )
)
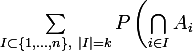 = \sum_{1\leq i_1<i_2<\ldots<i_k\leq n} P\left(A_{i_1}\cap A_{i_2}\cap\ldots\cap A_{i_k}\right))
Un autre point de vue, qui me semble bien adapté à la formule du crible où on considère toutes les intersection
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
