Calcul de somme à deux indices
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 28 Oct 2013, 22:14
par Romanouch » 28 Oct 2013, 22:14
Bonjour,
Voici le résultat auquel j'aboutis:
}=\frac{n^2.(3+n)}{2})
A la calculatrice (TI89), en faisant
})})
j'obtiens un résultat différent.
Quelqu'un peut-il me donner la bonne réponse et me donner la bonne façon d'utiliser la calculatrice pour calculer cette somme?
Merci d'avance.

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 28 Oct 2013, 22:29
par eratos » 28 Oct 2013, 22:29
Ton résultat est faux, à vue de nez j commence à i+1 :lol3:
(Pour l'utilisation de la calculette: voir avec qqun d'autre)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Oct 2013, 23:55
par capitaine nuggets » 28 Oct 2013, 23:55
Salut !
Pour commencer :
 <br />= \sum_{j=2} ^n \( \sum_{i=1}^{j-1} (i+j) \) <br />= \sum_{j=2} ^n \( (j-1)j + \sum_{i=1}^{j-1} i \)<br />= \sum_{j=2} ^n \( (j-1)j + \sum_{i=1}^{j-1} i \))
Enfin, je te rappelle que :
}{2})
(2n+1)}{6})
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 29 Oct 2013, 01:03
par deltab » 29 Oct 2013, 01:03
Bonsoir
Romanouch a écrit:Bonjour,
Voici le résultat auquel j'aboutis:
}=\frac{n^2.(3+n)}{2})
A la calculatrice (TI89), en faisant
})})
j'obtiens un résultat différent.
Quelqu'un peut-il me donner la bonne réponse et me donner la bonne façon d'utiliser la calculatrice pour calculer cette somme?
Merci d'avance.
L'erreur est dans l'écriture de la somme double:
}=\bigsum_{i=1}^{n}{(\bigsum_{j=i+1}^{n}{(i+j)})})
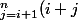=\bigsum_{j=i+1}^{n} i+\bigsum_{j=i+1}^{n}j}=i\bigsum_{j=i+1}^{n}1+ \bigsum_{j=i+1}^{n} j)
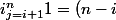i)
+(i+2)+...+n=(i+1)+(i+2)+...+(i+(n-i)))
i+\dfrac{(n-i)(n-i+1)}{2})
d'où
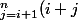=2(n-i)i+\dfrac{(n-i)(n-i+1)}{2})
et
}=\bigsum_{i=1}^{n}(2(n-i)i+\dfrac{(n-i)(n-i+1)}{2})=.....)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 29 Oct 2013, 11:58
par capitaine nuggets » 29 Oct 2013, 11:58
Faux : Dans la somme, on a
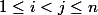
donc

va de

jusqu'à

et non pas

.
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 30 Oct 2013, 10:17
par Romanouch » 30 Oct 2013, 10:17
capitaine nuggets a écrit:Faux : Dans la somme, on a
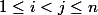
donc

va de

jusqu'à

et non pas

.
Bonjour à tous,
Je vous remercie pour vos réponses.
Je trouve
.n.(n+1)}{2})
(à la fois par le calcul et par la calculatrice)
Est-ce correct?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 30 Oct 2013, 11:13
par capitaine nuggets » 30 Oct 2013, 11:13
Romanouch a écrit:Bonjour à tous,
Je vous remercie pour vos réponses.
Je trouve
.n.(n+1)}{2})
(à la fois par le calcul et par la calculatrice)
Est-ce correct?
Oui, c'est bon ! :+++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
j'obtiens un résultat différent.
+(i+2)+...+n=(i+1)+(i+2)+...+(i+(n-i)))
i+\dfrac{(n-i)(n-i+1)}{2})
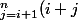=2(n-i)i+\dfrac{(n-i)(n-i+1)}{2})
(à la fois par le calcul et par la calculatrice)