Sujet des Nombres Complexes (Mini-Défi)

[othman2000]

Hello ,

Sujet Complet : (2 parties) (8questions)
PARTIE I :
a ∈ iIR et n ∈ IN (n≥2)
On considère l’équation : (E) :
On considère S l'ensemble des solutions de l'équation (E)
1) Montrez que :

2) Résoudre dans C l'équation (E)

3) On considère l'équation : (F) :
3-a) Montrez que les solutions de (F) appartiennent à IR
3-b) Résoudre dans C l’équation (F)

PARTIE II :
4) On pose : P(z) =
4-a) Déterminez la degré de la polynôme (P)
4-b) On pose : P(z) =
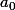
Trouvez en fonction de
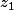
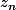
4-c) Soit et et .... les solutions de l'équation P(z)=0
Montrez que :
4-d) Conclure que :
(∀p ∈ IN*) :

[Lostounet]

Ya Habibi tu as déjà pris de mon temps pour que je te réponde sur l'autre topic...et là tu repostes le même sous un autre pseudo (hello from the other side?)

... Continue sur l'autre.