Bonjour,
je ne comprends pas bien la correction de la première question ( la I)a) ) de l'exercice 3 ici présent http://mp.cpgedupuydelome.fr/pdf/CCP%20MP%20-%20CCP%202011.pdf
Quelqu'un pourrait-il me donner quelques explications ? ( qu'est-ce qui permet d'affirmer que " A partir d'un certain rang [...] " )
Merci !
Suites équivalentes de même signe à partir d'un certain rang
3 messages
- Page 1 sur 1
Salut !
"À partir d'un certain rang [...]" est la même chose que "Il existe un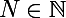 tel que pour tout entier
tel que pour tout entier 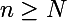 [...]".
[...]".
En particulier pour ton exercice, puisque tes deux suites sont équivalentes, il existe un rang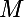 à partir duquel
à partir duquel 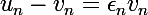 (*) avec
(*) avec ) une suite tendant vers 0. Or (*) se réécrit
une suite tendant vers 0. Or (*) se réécrit 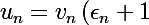) , et puisque
, et puisque ) tend vers 0, on peut la choisir aussi petite qu'on veut, en particulier puisqu'on veut que
tend vers 0, on peut la choisir aussi petite qu'on veut, en particulier puisqu'on veut que 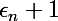 soit strictement positif ( pour ensuite conclure quant aux signes de
soit strictement positif ( pour ensuite conclure quant aux signes de 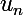 et
et 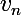 ), on peut par exemple chercher à imposer à
), on peut par exemple chercher à imposer à 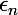 d'être inférieur en norme à
d'être inférieur en norme à  et il existe justement ( par définition de la limite ) un rang
et il existe justement ( par définition de la limite ) un rang 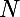 à partir duquel c'est vérifié. Après faut veiller à bien préciser que c'est le plus grand des deux rangs qu'on prend désormais ( bah ouais, faut vérifier les deux propositions en même temps, celle sur la traduction de l'équivalent et l'autre sur la contrainte imposée à
à partir duquel c'est vérifié. Après faut veiller à bien préciser que c'est le plus grand des deux rangs qu'on prend désormais ( bah ouais, faut vérifier les deux propositions en même temps, celle sur la traduction de l'équivalent et l'autre sur la contrainte imposée à 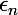 ).
).
"À partir d'un certain rang [...]" est la même chose que "Il existe un
En particulier pour ton exercice, puisque tes deux suites sont équivalentes, il existe un rang
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
