Suite f(un)=un

[Thecatz]

soit Un+1(a)=(exp(Un(a)))/(n+2)

Uo(a)=a

A est l'ensemble des valeurs de a pour lesquelles la suite (Un(a)) converge vers 0.

1) comment montrer que pour tout entier n la fonct° Un est croissante et continue sur R (réel).

2) Soit a€A, montrer que l'intervalle )- l'infini ; a) est inclus dans A.

3) Justifier l'existence d'une borne supérieur pour A.
soit w=supA, montrer que l'intervalle )- l'infini à w( est inclus dans A et que A est inclus dans )- l'infini ; a).

pour le 1) j'ai pensé à une récurence, mais pour les autres je en vois pas trop. Merci d'avance !

[Lierre Aeripz]

1. C'est bien une récurrence. Il reste à la rédiger.

2. Il faut utiliser la question 1 et les fait que les fonctions soit positives.

3. Il faut montrer que A est borné. Grâce à la question 2, il suffit de montrer qu'il existe un réel qui n'est pas dans A. A première vue, c'est un peu plus délicat.

[busard_des_roseaux]

bonjour TheCatz,

2)
Soit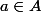
, on montre par récurrence
sur l'entier n que:



En appliquant le théorème des gendarmes, et en passant à la limite,
.

A est donc un intervalle.


2bis)
On montre que
majorée entraine en passant au log dans la formule de récurrence.

Puis,
On montre par récurrence sur l'entier n, que la propriété

est héréditaire.

donc:


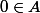
3)
On va montrer que 4 n'appartient pas à A.

à vérifier:
(I1 )

à vérifier à la main:





au dela du rang n=4:
la propriété est héréditaire par rapport à l'entier n d'après l'inégalité I1.
d'où:

4 n'appartient pas à A.
A est un intervalle majoré par 4.


Cordialement,