Suite

[Este]

Bonjour,
Dans un Dm , un exercice porte sur l’étude de la suite un+1= un+ exp(-un), dans la question précédente je devais étudier la monotonie de la suite, et j'ai trouvé qu'elle était croissante ensuite je dois maintenant Etudier, si elle existe, la limite de la suite (un), or je ne vois pas comment faire

[Este]

PS : je pense que la limite est +infini

[Ben314]

Salut,
- Si on suppose que ta suite est majorée, qu'en déduit-t-on ?
- Si on suppose que ta suite converge vers un certain réel L, que doit vérifier L ?
- Qu'en déduit tu ?
- Que peut-on dire d'une suite croissante et non majorée ?

[Este]

Si on suppose que la suite est majorée alors, on en déduit qu'il existe M ∈ R, ∀ A ∈ N, ∀ n>=A, un< M, donc on a aussi un+1 < M d'ou un+exp(-un)<M
Si on suppose que la suite converge vers un réel L on a donc L<M
Mais je ne vois pas ce que je peux en déduidre de plus

[pascal16]

Un+1=f(Un)

f est continue, quelle equation vérifie la limite si elle existe ?

[Este]

lim f= L ?

[pascal16]

tu as vu le théorème du point fixe ?

[Este]

Ce nom ne me dis rien

[pascal16]

x+exp(x) >=1

pour toute valeur de Uo, on a U1>=1

à partir de là, tu dois pourvoir prouver que Un+1-Un >=1

Un va être dure à majorer

[Este]

Mais Un+1-Un>=1 montre seulement que la suite est croissante pas qu'elle n'est pas majorée ou je me trompe ?
par contre la suite est Un+exp(-Un) et pas Un+exp(Un)

[Este]

PS : on connait U0=0

[pascal16]

Soit Vn une suite telle que
Vo = 0
Vn+1 = 1 +Vn
tu as Vn = n

et Un >= Vn <- pas bon

[Este]

Comment deduisez que Vn=n ? et que Un>=Vn ?

[pascal16]

erreur de ma part, on a pas Un+1-Un >=1.

[Este]

Je ne comprends pas ou voulez en venir avec Un+1-Un

[pascal16]

Vn+1 -Vn >0 donne la strict croissance
Vn+1-Vn > a, a constante strictement positive => Vn minorée par suite arithmétique de raison >0, donc de limite oo.

mais c'est pas le cas ici.

[Este]

Donc si Vn+1-Vn > a, a constante strictement positive, Vn est minorée par suite arithmétique de raison >0, donc sa limite est +oo c'est ca ?

[pascal16]

Un+1-Un= exp(-Un).

Un >1 pour n >=2
si Un converge vers l , on a l>=1
il existe donc no tel que l-0.5<Un< l+0.5

pour n>no
(il faut normalement soit parler de queue de suite ou de Vn=Un-no)
Un+1-Un= exp(-Un)
donc exp(-l-0.5) <Un+1-Un< exp(-l+0.5)
d'où un encadrement de Un+1-Un par deux suites arithmétiques tendant vers +oo

[aviateur]

Bonjour
La suite est strictement croissante (OK) donc soit elle converge vers un nombre réel l ou alors elle tend vers l'infini.
Si elle converge vers l: puisque on a pour tout n,
alors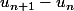 va tendre vers l-l=0 et va tendre vers
Par unicité de la limite cela implique que ce qui est impossible.
Par conséquent la suite diverge vers + l'infini.

Question subsidiaire. Pour quelle valeur de n aura-t-on