Suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Aoû 2018, 00:28
par mehdi-128 » 13 Aoû 2018, 00:28
Bonsoir,
Je bloque toujours sur ce genre de question et là encore une fois alors que je sais que c'est pas dur

La suite
)
est définie sur

J'ai :
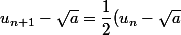)
Et je veux exprimer
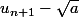
en fonction de

J'ai fait :
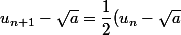 = (\dfrac{1}{2} )^2(u_{n-1} - \sqrt{a} )=(\dfrac{1}{2} )^3(u_{n-2} - \sqrt{a} ))
En fait quand je vais arriver à

je n'arrive pas à savoir quelle va être la puissance sur le

-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 13 Aoû 2018, 07:36
par pascal16 » 13 Aoû 2018, 07:36
Ilk faut faire propre
Vn= Un-√a
Vn : suite géométrique
Vo= ...
d'où Vn= ...
d'où Un=....
et quand tu aura l'habitude, il passera de la première à la dernière ligne
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 13 Aoû 2018, 09:36
par Pseuda » 13 Aoû 2018, 09:36
Bonjour,
A chaque pas, l'exposant de 1/2 + l'indice de u est constant égal à n+1. Quand on arrive à u0, cela fait donc (1/2)^(n+1).
Ou bien l'indice de u passe de n+1 à 0, donc descend de n+1. L'exposant de 1/2 passe alors de 0 à n+1 (il augmente de n+1).
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Aoû 2018, 11:55
par mehdi-128 » 13 Aoû 2018, 11:55
pascal16 a écrit:Ilk faut faire propre
Vn= Un-√a
Vn : suite géométrique
Vo= ...
d'où Vn= ...
d'où Un=....
et quand tu aura l'habitude, il passera de la première à la dernière ligne
Merci

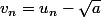
donc :
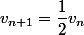
)
est une suite géométrique de raison
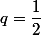
donc :
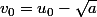
et
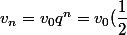^n)
Donc :
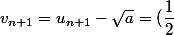 ^{n+1} (u_0 - \sqrt{a}))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Aoû 2018, 11:56
par mehdi-128 » 13 Aoû 2018, 11:56
Pseuda a écrit:Bonjour,
A chaque pas, l'exposant de 1/2 + l'indice de u est constant égal à n+1. Quand on arrive à u0, cela fait donc (1/2)^(n+1).
Ou bien l'indice de u passe de n+1 à 0, donc descend de n+1. L'exposant de 1/2 passe alors de 0 à n+1 (il augmente de n+1).
Merci, j'ai bien fait de demander, mon livre avait une coquille c'était écrit 1/2 puissance n au lieu de n+1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités