Suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Porbleme_serie » 12 Fév 2014, 20:57
par Porbleme_serie » 12 Fév 2014, 20:57
Bonsoir,
pourriez vous m'aider pour un exercice que je n'arrive pas du tout à faire, d'où ma demande d'aide.
Enoncé:Si
_{n\geq0})
une suite numérique qui tend vers 0 et x,y,z des réels où
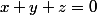
.
Pour tout
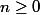
:
 Question:
Question: montre que la suite

converge.
Et calculer sa somme.
Merci à ceux qui m'aideront.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 12 Fév 2014, 22:04
par Sa Majesté » 12 Fév 2014, 22:04
Salut
Tu sais que (wn) converge vers 0 donc tu peux traduire ça avec des epsilon.
Et après tu majores|un|.
 par Porbleme_serie » 12 Fév 2014, 22:10
par Porbleme_serie » 12 Fév 2014, 22:10
Sa Majesté a écrit:Salut
Tu sais que (wn) converge vers 0 donc tu peux traduire ça avec des epsilon.
Et après tu majores|un|.
Bonsoir et merci pour l'aide.
Pourriez vous me donner plus de détails sur un point, je ne vois pas ce que vous voulez dire par "traduire avec des epsilons".
 par Porbleme_serie » 13 Fév 2014, 11:27
par Porbleme_serie » 13 Fév 2014, 11:27
Re
Pourriez vous svp me préciser la partie que je n'ai pas compris.
Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 13 Fév 2014, 12:24
par Monsieur23 » 13 Fév 2014, 12:24
Aloha,
Tu parles de la
série 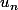
?
« Je ne suis pas un numéro, je suis un homme libre ! »
 par Porbleme_serie » 13 Fév 2014, 13:39
par Porbleme_serie » 13 Fév 2014, 13:39
Monsieur23 a écrit:Aloha,
Tu parles de la
série 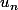
?
salut,
bizarrement, c'est un exercice inscrit dans le thème des séries, mais l'exercice parle bien de suite et non de série.Il s'agit peut être d'une erreur alors.
J'ai marqué exactement l'intitulé de l'énoncé.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 13 Fév 2014, 13:55
par Monsieur23 » 13 Fév 2014, 13:55
Porbleme_serie a écrit:salut,
bizarrement, c'est un exercice inscrit dans le thème des séries, mais l'exercice parle bien de suite et non de série.Il s'agit peut être d'une erreur alors.
J'ai marqué exactement l'intitulé de l'énoncé.
Ça doit être une erreur :
la suite (u_n) tend clairement vers 0 (w_n tend vers 0, w_n+1 et w_n+2 aussi
)
pour la question suivante, on ne peut pas calculer la somme d'une suite
À mon avis, essayes plutôt de montrer que la série converge
« Je ne suis pas un numéro, je suis un homme libre ! »
 par Porbleme_serie » 13 Fév 2014, 14:03
par Porbleme_serie » 13 Fév 2014, 14:03
Je suis également d'avis que c'est une erreur, et que l'on cherche la somme d'une série.
Pourriez vous m'expliquer svp, la réponse de
Sa Majesté:
>Sa Majesté: Tu sais que (wn) converge vers 0 donc tu peux traduire ça avec des epsilon.
Et après tu majores|un|.
car je ne comprend pas ce qu'il veut dire pas traduire la convergence en zéeo avec des epsilon.
Merci.
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 13 Fév 2014, 14:16
par Tiruxa » 13 Fév 2014, 14:16
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 13 Fév 2014, 14:17
par Monsieur23 » 13 Fév 2014, 14:17
Il te propose de montrer que la suite u_n tend vers 0 en utilisant la définition formelle de limite (pour tout epsilon>0, il existe N tel que pour tout n>N, |u_n| < epsilon).
« Je ne suis pas un numéro, je suis un homme libre ! »
 par Porbleme_serie » 13 Fév 2014, 14:24
par Porbleme_serie » 13 Fév 2014, 14:24
Merci Tiruxa pour ta réponse détaillé, et merci Monsieur23 car je n'avais pas compris qu'il fallait utiliser la définition formelle de limite.
Merci à tous.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Fév 2014, 23:32
par deltab » 13 Fév 2014, 23:32
Bonsoir
@Tiruxa
On pouvait rendre les sommes télescopiques plus "visibles" en écrivant:
 =\sum_{k=0}^n (x(w_k-w_{k+2})+y(w_{k+1}-w_{k+2})))
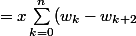+y\sum_{k=0}^n (w_{k+1}-w_{k+2})=x(w_0+w_1-w_{n+1}-w_{n+2})+y(w_1-w_{n+2}))
Ps: Si la suite
)
est convergente vers une limite

pas nécessaiment nulle, la série

reste convergente et de somme
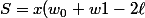+y(w_1-\ell))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités