Suite Un= A^(n+1) / B^n

[yavit]

bonjour je suis a la recherche de documentation a propos d'une série

Un= A^(n+1) / B^n

A et B étant des nombres réel

et est ce que cette suite reponds a la condition suivante

Un+1 - Un = Un+2 -Un+1



merci d'avance

[fatal_error]

salut,

ben, en posant B = 1 et A=2,
u_n = 2^(n+1)

et je doute quelle satisfasse la condition Un+1 - Un = Un+2 -Un+1

[JeanJ]

Un= A^(n+1) / B^n
Soit C=A/B et Vn = Un/A
Vn = C^n

[Black Jack]

U(n) = A^(n+1) / B^n

U(n+1) = A^(n+2) / B^(n+1)

U(n+1)/U(n) = A/B

...

Cela ne répond pas à la question que tu as posé ... mais peut-être à celle que tu aurais du poser.

:zen:

[fatal_error]

pis tant qu'a faire pour déterminer les valeurs de A et B qui vérifient la condition.
On pose
soit pour la condition

donc et on déduit

qui est une suite arithmétique de raison
soit (1)
avec
et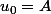
soit depuis (1)


Pour A différent de 0 (qui donne une solution ). En posant on a

soit


Reste à cherche la valeur de C qui satisfait lequation qqsoit n.
Trivialement si C = 1, alors c'est good.

Etude de la fonction

si x>0, f'(x) est positive, et strictement croissante donc x=1 est seule solution.
si x négatif on teste pour valeurs successives de n :
n pair :
C^n est positif, et n(C-1) est negatif donc c'est dead.

[yavit]

grand merci a tous ceux qui ont répondu , votre aide m'a été très précieuse


thanks