Suite infinie 1-1/2+1/3-1/4....-> ln(2)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
par Anonyme » 21 Avr 2006, 18:53
Bonjour je cherche desesperement la demonstration de
1-1/2+1/3-1/4....(-1)^(n+1)*1/n -> ln(2)
Apres une heure de blocage et de lutte insoutenable je n'ai rien obtenue de trés convaincant...notament en utilisant une suite définie par recurrance comme
U(n+1) = - n/(n+1) * Un
puis la formule des suites géométriques...
http://www.maths-forum.com/newthread.php?do=newthread&f=15#Hum
Merci
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 21 Avr 2006, 19:02
En intégrant :
=x-\frac{x^2}{2}+\frac{x^3}{3}-...)
Si x=1, ln(2)= ... (série semi convergente)
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
par abcd22 » 21 Avr 2006, 19:08
Bonsoir !
On peut calculer la limite en écrivant
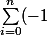^i x^i = \frac{1}{1+x} + (-1)^n \frac{x^{n+1}}{1+x})
pour x entre 0 et 1. On intègre des deux côtés entre 0 et 1 et on trouve le résultat en faisant tendre n vers l'infini.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
