Suite à indice double

[egan]

Salut tout le monde,

Est-ce qu'il est vrai que ce truc là tend vers 0 quand tend vers :



Je pense que non mais je ne vois pas spécialement comment le justifier.
En fait le problème revient à montrer que le troisième membre de la somme tend vers 0.

Y a -t-il des méthodes pour gérer ces fonctions à deux variables ?

Merci d'avance.
@+ Boris.

[Le_chat]

T'es sur que c'est quand ça tend vers 0? Vu que là le premier terme a une tendance à tendre vers l'infini!

[egan]

Oups, erreur d'énoncé. La norme tend vers l'infini.

[girdav]

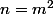
Tout se ramène à voir si converge vers 0 quand . Le problème est que si l'on prend , l'expression est , et cette quantité tend vers l'infini.

Si la quantité de départ tendait vers , ça serait le cas si le couple tend vers l'infini de la manière .

(je suppose que le problème vient de la vérification qu'une suite particulière est de Cauchy, et que tu as du majorer trop brusquement. Est-ce que tu peux donner la suite en question ?)

[egan]

Je m'étais dit que ça ne pouvait pas marcher pour cette raison mais je n'étais pas sûr.

Effectivement, je cherchais à montrer qu'une certaine suite était de Cauchy:

La norme est la norme L^2([-1;1]) et la suite f_n vérifie:

f_n(x) = 0 si x dans [-1;-1/n]
f_n(x) = nx+1 si x dans [-1/n;0]
f_n(x) = 1 si x dans [0;1]