Je ne suis pas sûr qu'on puisse dire que la suite
)
vérifie ce que tu as écrit, car

est dénombrable et

ne l'est potentiellement pas.
Je ne connais pas bien les nets. L'idée que j'avais était celle-ci :
)
est une suite de Cauchy, donc converge vers une certaine limite

Fixons

, on a donc un indice
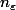
tel que l'inverse est inférieur à

et on a donc l'existence d'un indice
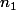
supérieur tel que
<\varepsilon)
Si on appelle

l'antécédent de
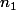
par

, on a donc
<\varepsilon)
Mais également, il existe un indice
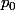
(que l'on peut prendre supérieur à

) tel que pour tout p,q qui lui sont supérieurs, on a
<\varepsilon)
En particulier
<\varepsilon)
Or
<=d(x_p,x_{p_1})+d(x_{p_1},\lambda)<2\varepsilon)
D'où : pour tout

, il existe un rang

tel que pour tous les p qui lui sont supérieurs, on a
<2\varepsilon)
(Mais je ne sais pas si c'est bien cela la définition de la limite pour une suite généralisée)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
