Suite des noyaux itérés
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 24 Juin 2008, 16:27
Bonjour!
Voilà l'exo classique sur lequel je me prend actuellement la tête.
Soit
)
. Montrer que
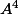
et
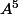
ont même rang.
J'aimerais pour cela utiliser le résultat sur les noyaux itérés d'un endomorphisme (croissants pour l'inclusion et constant a.p.d.c.r) seulement je n'arrive pas à comprendre pourquoi on aurait
=ker(a^5))
(résultat qui semble à priori provenir de la dimension de
)
...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 24 Juin 2008, 17:31
Regarde la suite des noyaux de
.
Que dire si elle est strictement croissante?
Que dire dans l'autre cas?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 24 Juin 2008, 17:34
Aspx a écrit:Bonjour!
Voilà l'exo classique sur lequel je me prend actuellement la tête.
Soit
. Montrer que
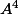
et
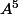
ont même rang.
J'aimerais pour cela utiliser le résultat sur les noyaux itérés d'un endomorphisme (croissants pour l'inclusion et constant a.p.d.c.r) seulement je n'arrive pas à comprendre pourquoi on aurait
(résultat qui semble à priori provenir de la dimension de
...
Suffit de savoir compter jusqu'à 5 ....
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 24 Juin 2008, 17:59
On sait déjà que les noyaux vérifient
[CENTER]
[/CENTER]
Si la croissance est stricte, on a forcément
[CENTER]
[/CENTER]
donc
ou
. Ensuite on obtient deux contradiction et la conclusion puisque l'égalité des noyaux se transmet à
. C'est correct ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 24 Juin 2008, 18:12
Aspx a écrit: ou
.
J'avais même pas envisagé le premier cas (il est impossible car si le premier noyau est trivial,
est un isomorphisme et ses puissances aussi)
Le seul cas est "1<2<3<4" qui conduit à
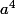
nul donc
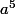
nul aussi.
Maintenant que dire si la suite est pas strictement croissante?
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 24 Juin 2008, 18:23
Si elle n'est pas strictement croissante on a
[CENTER]
[/CENTER]
Mais alors
[CENTER]
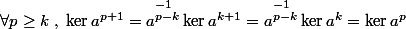
[/CENTER]
En particulier on a
Donc vu le théorème du rang
[CENTER]
[/CENTER]
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 24 Juin 2008, 19:49
C'est
que
.
Ensuite tu as
et tu composes par
de chaque côté. Je trouve que c'est mieux qu'avec les images réciproques, mais bon...
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 24 Juin 2008, 20:04
yos a écrit:C'est
que
.
Ensuite tu as
et tu composes par
de chaque côté. Je trouve que c'est mieux qu'avec les images réciproques, mais bon...
Entièrement d'accord ! Je te remercie pour ton aide :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
