Suite de Cauchy
14 messages
- Page 1 sur 1
Suite de Cauchy
bonsoir,
Si $x_{2}$ est une suite de CAUCHY AVEC $d(x_{n},x_{n+1})$ converge vers 0 alors la suite (x_{n}) est de Cauchy . Avec d une véréfie les propriètés d'une distance sauf elle est pas symétrique. J'arrive pas à démontrer ça quelqu'un peut m'aider et merçi
Si $x_{2}$ est une suite de CAUCHY AVEC $d(x_{n},x_{n+1})$ converge vers 0 alors la suite (x_{n}) est de Cauchy . Avec d une véréfie les propriètés d'une distance sauf elle est pas symétrique. J'arrive pas à démontrer ça quelqu'un peut m'aider et merçi
Re: Suite de Cauchy
Salut,
Juste pour t'informer que les bonnes balises à utiliser pour les formules sont : "[TEX ] ..... [/TEX ] (sans les espaces)
(:
Juste pour t'informer que les bonnes balises à utiliser pour les formules sont : "[TEX ] ..... [/TEX ] (sans les espaces)
(:
Re: Suite de Cauchy
Bon, d'abord tu vas faire un effort en appliquant en particulier la remarque de @Yezu
afin que l'on puisse lire et comprendre ta question sans se casser la tête.
Ensuite il y bien quelqu'un qui te répondra.
afin que l'on puisse lire et comprendre ta question sans se casser la tête.
Ensuite il y bien quelqu'un qui te répondra.
Re: Suite de Cauchy
bonjour,
est ce que tu dois démontrer que si_{n \in \mathbb{N}}) est de Cauchy et
est de Cauchy et
= 0) alors la suite
alors la suite _{n \in \mathbb{N}}) est de Cauchy.
est de Cauchy.
ou un autre résultat ?
est ce que tu dois démontrer que si
ou un autre résultat ?
Re: Suite de Cauchy
soit 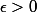
il existe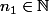 pour tout
pour tout 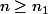 , pour tout
, pour tout 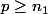
 \leq d(x_{2p+1};x_{2p})+d(x_{2p};x_{2n})+d(x_{2n};x_{2n+1}) <br />\leq \dfrac{\epsilon}{3}+\dfrac{\epsilon}{3}+\dfrac{\epsilon}{3} \leq \epsilon)
d'après les hypothèses.
les autres cas se traitent de la même façon.
il existe
d'après les hypothèses.
les autres cas se traitent de la même façon.
Re: Suite de Cauchy
Salut,
pour la distance d, je noterai en valeur absolue pour que ça soit plus lisible....
Soit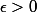 .
.
Comme) est de Cauchy, il existe
est de Cauchy, il existe  entier tel que pour tout
entier tel que pour tout 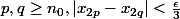 . (*)
. (*)
Comme_n) tend vers 0, il existe
tend vers 0, il existe 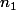 entier tel que pour tout
entier tel que pour tout 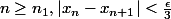 (**)
(**)
Posons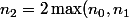) .
.
Prenons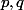 deux entiers tels que
deux entiers tels que 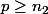 et
et 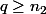 et montrons que
et montrons que 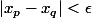 .
.
Si p et q sont pair, alors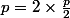 et
et 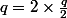 et comme
et comme 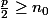 et
et 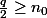 , le résultat s'ensuit d'après (*).
, le résultat s'ensuit d'après (*).
Si p est pair et q impair. Alors on écrit :
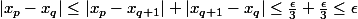 .
.
Première inégalité car p, q+1 sont tous deux pairs et p/2 et (q+1)/2 sont tous deux supérieurs à .
.
Deuxième inégalité car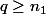 et en utilisant (**).
et en utilisant (**).
Enfin, si p et q sont tous deux impairs, alors
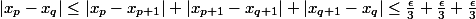 d'après (*) puis (**) puis (*).
d'après (*) puis (**) puis (*).
PS : mathelot plus rapide.
pour la distance d, je noterai en valeur absolue pour que ça soit plus lisible....
Soit
Comme
Comme
Posons
Prenons
Si p et q sont pair, alors
Si p est pair et q impair. Alors on écrit :
Première inégalité car p, q+1 sont tous deux pairs et p/2 et (q+1)/2 sont tous deux supérieurs à
Deuxième inégalité car
Enfin, si p et q sont tous deux impairs, alors
PS : mathelot plus rapide.
Pseudo modifié : anciennement Trident2.
Re: Suite de Cauchy
Merç pour votre réponse j'ai une tout petite remarque si l'appliaction d ne vérifie pas la condition de la symètrie comment on peut obtenir le résultat dans la cas où p et q sont impairs
Re: Suite de Cauchy
Si, car je n'ai que )) qui converge vers 0 et pour la deuxième i.e
qui converge vers 0 et pour la deuxième i.e )) je n'ai aucun idèe sur cette suite là comment peut on montrer que si
je n'ai aucun idèe sur cette suite là comment peut on montrer que si 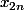 est de cauchy alors
est de cauchy alors  l'est aussi
l'est aussi
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
