Suite de cauchy, définition des réels

[lapras]

Bonsoir,
est ce que quelqun peut m'expliquer le plus simplement possible les suites de cauchy et la définition des nombres réels ?
Ou alors me donner l'adresse d'un cour simple dessus.
Merci d'avance
Lapras

[ThSQ]

Est-ce que tu connais la construction de Z et Q, les espaces quotient, ... ?

http://www.dma.ens.fr/culturemath/maths/pdf/logique/reels.pdf

[Nightmare]

Salut :happy3:

En gros une suite de Cauchy c'est une suite telle qu'à partir d'un certain rang, les termes sont aussi proches que l'on veut les uns des autres.

A priori on a l'impression que les suites de Cauchy sont convergentes. En fait ce n'est pas tout le temps vrai, mais un espace dans lequel toute suite de Cauchy converge est appelé espace complet (R par exemple est complet).

Concernant la construction de R, c'est en gros une exstention de Q construite par nécessité de pouvoir identifier les irrationnels comme e, pi ou même racine de 2.

Tu trouveras plus de détail sur cette construction sur internet.

:happy3:

[Joker62]

Moi j'applaudis la blague de Rain'
Elle est quand même excellente !

[Antho07]

Moi j'applaudis la blague de Rain'
Elle est quand même excellente !

C'est vraiment qu'elle est pas mal. :we:

Bien trouvé.


Elle nécessite néanmoins quelques connaissances pour la comprendre.

Faudrais rajouter "quelque part dans le monde réel".

Si c'est trop rationnel cela marche plus.

[kazeriahm]

salut

pour rajouter un peu à ce qui a été dit :

les suites de Cauchy forment une classe de suite aux propriétés intéressantes : elles sont bornées, si elles possèdent une valeur d'adhérence alors elles convergent vers cette valeur d'adhérence, toute suite convergente est de Cauchy, ...

qu'un espace soit complet (comme l'a déjà dit Nightmare un espace complet est un espace dans lequel toute suite converge) donne lieu à des théorèmes de topologie et d'analyse très forts

les R ou C-espaces vectoriels de dimension finie sont complets (R,R^2,C^157,...)

[busard_des_roseaux]

Bonjour,

Il y a plusieurs constructions de possibles. Soit , à partir de rien, directement, selon une numérotation des étapes de création (les nombres du 1er jour, du second jour,..) , comme le fait Conway dans "surreals numbers", soit par les coupures (Richard Dedekind), qui définit un nombre réel comme la paire de deux ensembles non vides de rationnels adjacents (1858).
est vû comme la paire des deux ensembles de rationnels

qui n'ont ni plus grand , ni plus petit élément.

On fait la construction suivante:
1°) les suites de Cauchy forment un anneau pour l'addition et la multiplication.
Elles sont bornées.
1°) les suites de limite nulle, constituent un sous-anneau des suites de Cauchy de rationnels et même en constituent un idéal.
2°) est vû comme le quotient de l'anneau des suites de rationnels de Cauchy par cet idéal.
3°) addition et multiplication passe au quotient. L'archimédianité est conservée.
3°) On identifie au sous-ensemble des suites de rationnels constantes à partir d'un certain rang.

Ensuite, on constate que l'ensemble ainsi construit est connexe , alors que est totalement discontinu et
que est équipotent à l'ensemble des parties de (Georg Cantor). Paul Cohen a prouvé, par la suite :zen: , en 1963, que l'existence d'un cardinal, strictement compris entre et , est indémontrable.

Une suite remarquable qui ne vérifie pas le critère de Cauchy, est la série harmonique.

souffre d'un défaut: il n'est pas algébriquement clos,
ce qui conduit au corps des nombres complexes, mais on perd alors la relation d'ordre.

Aujourd'hui, on fait de l'analyse dite "non standard", où, en plus des nombres réels, on considère des "infinitésimaux". Les nombres restent donc un domaine en constante évolution et remaniement depuis l'Antiquité.

[Aspx]

C'est deux suites de Cauchy qui vont en boite, à la soirée ''No Limit''. Mais à l'entrée, elles tombent sur le vigil qui leur dit : ''désolé, c'est complet"...

Désolé :triste: :marteau:

Enorme :ptdr:

[lapras]

Bonjour,
1°) les suites de limite nulle, constituent un sous-anneau des suites de Cauchy de rationnels et même en constituent un idéal.
2°) est vû comme le quotient de l'anneau des suites de rationnels de Cauchy par cet idéal.
3°) addition et multiplication passe au quotient. L'archimédianité est conservée.
3°) On identifie au sous-ensemble des suites de rationnels constantes à partir d'un certain rang.

Ensuite, on constate que l'ensemble ainsi construit est connexe , alors que est totalement discontinu et
que est équipotent à l'ensemble des parties de (Georg Cantor). Paul Cohen a prouvé, par la suite :zen: , en 1963, que l'existence d'un cardinal, strictement compris entre et , est indémontrable.

Une suite remarquable qui ne vérifie pas le critère de Cauchy, est la série harmonique.

souffre d'un défaut: il n'est pas algébriquement clos,
ce qui conduit au corps des nombres complexes, mais on perd alors la relation d'ordre.

Aujourd'hui, on fait de l'analyse dite "non standard", où, en plus des nombres réels, on considère des "infinitésimaux". Les nombres restent donc un domaine en constante évolution et remaniement depuis l'Antiquité.

merci à tous ! mais dans le message de busard_des_roseaux je ne connais pas les mots en gras. Donc je ne peux pas comprendre son message.
Peux tu les définir ?

[kazeriahm]

salut

un ensemble A est un anneau si, par définition, il est muni de deux lois de compositions internes notées + et *, telles que (A,+) est un groupe, * est associative, distributive sur + (Z,+,*) est un anneau par exemple

si A est un anneau et B C A, B est un sous anneau de A si (B,+,*) est un anneau

si A est un anneau commutatif (c'est à dire que la loi * est commutative) et I C A, on dit que I est un idéal de A si (I,+) est un sous-groupe de (A,+) et si pour tout a € A et i € I, a*i € I

par exemple dans Z, les ensembles de la forme nZ sont des idéaux de Z (et par ailleurs ce sont les seuls idéeaux de Z)

[Skullkid]

Salut, je vais essayer de te les définir :

Anneau : C'est une structure algébrique, en gros c'est un ensemble dans lequel on peut faire des additions, des soustractions et des multiplications (mais pas forcément des divisions).
Exemple : l'ensemble des fonctions de dans lui-même avec les lois d'addition et de composition est un anneau.

Sous-anneau : Sous-ensemble d'un anneau qui, muni des mêmes lois, est un anneau.

Idéal : Sous-anneau I d'un anneau A qui vérifie :
(où xy désigne le produit de x par a via la loi multiplicative de l'anneau).
En gros, c'est un sous-anneau de A qui "absorbe" les éléments de A par multiplication.

Anneau quotient : Soit un anneau A et I un idéal de A. On définit la relation d'équivalence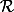 par :

L'anneau quotient A/I est alors l'ensemble des classes d'équivalence des éléments de A par la relation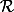 (la classe d'équivalence d'un élément x de A est l'ensemble des éléments de A qui sont en relation avec x)
Exemple :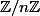 est un anneau quotient, c'est l'ensemble des classes d'équivalence des entiers modulo n, ie par la relation

Connexe : Un ensemble est connexe s'il est "en un seul morceau". Exemple :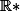 n'est pas connexe.

Equipotent : Deux ensembles sont équipotents s'il existe une bijection de l'un sur l'autre.

Voilà, je crois qu'il y a tout. Mais c'est juste des définitions en gros, y a des points que j'ai pas mentionnés. Pour en savoir plus je te renvoie à Wikipedia and co, en éspérant t'avoir un peu aidé

[lapras]

Tout d'abord merci a vous deux pour les explications.
Je ne comprend pas bien ce que signifie concretement x - y appartient à I

[Skullkid]

x et y sont des éléments de A, et x - y est un autre élément de A, mais il n'a aucune raison d'appartenir à I qui est un sous-ensemble de A. Si jamais x - y appartient à I, alors x et y sont en relation via .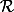

Par exemple pour et :
3 - 1 = 2 appartient à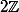 : 1 et 3 sont en relation.
3 - 2 = 1 n'appartient pas à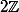 : 2 et 3 ne sont pas en relation.
Plus généralement on voit que deux entiers sont en relation ssi ils ont même parité, on définit donc 2 classes d'équivalence : celle des entiers pairs, qu'on note en général , et celle des entiers impairs, qu'on note .
On définit ainsi l'ensemble des entiers modulo 2.

[alben]

Bonsoir
C'est extraordinaire, je viens de parcourir ce fil et en réponse à une demande d'explication "simple", tous les sujets ont été évoqués.
Pour faire simple, maitriser toutes les notions introduites dans cette discussion devrait permettre à Lapras d'atteindre un niveau très largement supérieur à la compréhension de la construction des réels.
C'est pourquoi je me permet d'y mêler mon grain de sel en espérant simplifier quitte à faire quelques courts circuits que les puristes auront le droit de me reprocher :we:
1 La notion de base est celle de suite de Cauchy : comme l'a dit Nightmare,c'est une suite dont les termes se rapprochent de plus en plus. Elle devrait donc converger. Le problème, c'est que converger ça veut dire se rapprocher d'une limite qui appartienne à l'ensemble sur lequel on travaille.
Par exemple la suite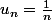 voit bien les se rapprocher et l'on comprend qu'elle devrait converger vers 0. Pourtant dans l'intervalle ]0;1] elle n'a pas de limite puisque zéro n'en fait pas partie.
2 La deuxième idée c'est de dire "considérons l'ensemble de toutes les suites de Cauchy et disons que deux suites sont équivalentes si 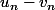converge vers zéro".
3 Et finalement une nombre réel c'est l'ensemble de toutes les suites qui convergent vers une même limite (attention, petit abus de langage, si la limite n'est pas rationnelle, on ne peut pas parler de limite ni de convergence)
Par exemple, 0, c'est un ensemble constitué de la suite 1/n mais aussi 1/n² et aussi 0,0,0...
Ca peut te paraître un peu bizarre pourtant tu pratiques une démarche identique avec les fractions quand tu considères que 0,5 c'est 1/2 et aussi 2/4 et aussi 127/254 etc...
3 et la phase finale, c'est d'assimiler le nombre 2, la fraction 8/4 et la suite (1;3/2;5/3;7/4;9/5.....). Ce sont différentes façons de décrire le même objet mathématique.

NB Ainsi, par définition d'un réel, 0,9999999... est exactement identique à 1
NB1 Ce n'est pas la seule façon de construire les réels

[lapras]

Oui Skullkid je comprend maintenant.
Cependant je n'arrive pas a comprendre la construction des réels avec cauchy.
Si j'ai bien compris, l'ensemble des suites convergentes est une sous partie de l'ensemble des suites de Cauchy.
Mais apres je vois mal le lien avec la construction des réels...

1°) les suites de limite nulle, constituent un sous-anneau des suites de Cauchy de rationnels et même en constituent un idéal.

Ok, il me semble logique que l'ensemble des suites de limite nulle forment un idéal de l'ensemble des suites de cauchy.

2°) IR est vû comme le quotient de l'anneau des suites de rationnels de Cauchy par cet idéal.

La c'est abstrait (enfin, ca fait bizarre, surtout que je commence tout juste à voir le vocabulaire)
si je reprend ta définition,
On se donne I l'idéal: ensemble des suites de limite nulles de cauchy
On prend l'anneau des suites de rationnels de Cauchy, et on détermine l'ensemble des classes d'équivalence pour chaque suite de rationnel de Cauchy, donc ca voudrait dire que pour une suite donnée U_n , on prend toutes les suites Vi_(n) telles que
lim Un - Vi_n = 0
n->+OOne
donc a chaque chaque classe d'équivalence des U_n est l'ensemble des suites ayant même limite que U_n ?

Merci de m'éclairer
Lapras

[lapras]

Je viens de voir ton message alben, merci pour ces explications (ca répond en partie à mes questions dans mon message précédent)
Ainsi 1 a deux développements décimal infini, c'est amusant.
j'ai vu le développement décimal infini, la troncature de Q en deux, et enfin Cauchy, mais on m'a conseillé cauchy donc je me concentre plus sur cauchy.

[alben]

En fait, la démarche de construction de R par les suites de Cauchy est identique à celle de la construction des rationnels.
1 On part des couples ZxZ* et on dit que (a/b) équivaut à (c/d) si ad-bc=0.
2 Chaque classe (=ensemble des couples équivalent) est un élement de Q.
3 On assimile les éléments r de Z à la classe qui contient le couple (r/1)
4 On verifie que tout ça reste bien cohérent avec les opérations usuelles (par exemple que si (a/b)+(c/d)=(e/f) le remplacement de chaque terme par un équivalent (a'/b')+(c'/d') nous donne un résultat équivalent. C'est fastidieux mais pas difficile.
5 Et on constate que les termes non nuls sont inversibles.
La manipulation des suites est un peu plus lourde mais la façon globale de faire est exactement la même.

[prody-G]

1 La notion de base est celle de suite de Cauchy : comme l'a dit Nightmare,c'est une suite dont les termes se rapprochent de plus en plus. Elle devrait donc converger. Le problème, c'est que converger ça veut dire se rapprocher d'une limite qui appartienne à l'ensemble sur lequel on travaille.
Par exemple la suite voit bien les se rapprocher et l'on comprend qu'elle devrait converger vers 0. Pourtant dans l'intervalle ]0;1] elle n'a pas de limite puisque zéro n'en fait pas partie.

je ne suis pas tout à fait d'accord avec ta définition de converger...la limite n'appartient pas forcément à l'ensemble en question mais à son adhérence. Et 0 appartenant à l'adhérence de ]0,1], 0 est effectivement la limite de .

[xyz1975]

je ne suis pas tout à fait d'accord avec ta définition de converger...la limite n'appartient pas forcément à l'ensemble en question mais à son adhérence. Et 0 appartenant à l'adhérence de ]0,1], 0 est effectivement la limite de .

Donc à ce moment là la suite converge dans Q puisque sa limite est bien l'exponentielle qui appartient à l'adhérence de Q et dans ce cas pourquoi alors se casser la tête et définir les éspaces complets.
On dit qu'une suite d'un espace E[ muni d'une distance (ou norme ou alors produit scalaire, en général d'un moyen de mesure)] est convergente s'il existe un element de E tel que ........