Suite de cauchy et convergence

[Clise]

Bonjour,

Bon alors voila, j'aurais une petite question de ... cours.

En topologie, nous pouvons démontrer qu'une suite convergente dans X est de Cauchy dans X. Cependant, "la réciproque est fausse".

Auriez vous un contre exemple de suite de Cauchy non convergente dans un espace métrique?

[ThSQ]

1/n dans (IR*,|.|) par exemple

[Clise]

Ok, mais elle est convergente dans (IR,| |). Ma question, surement mal formulée, était en fait existe il une suite de cauchy mais qui ne converge pas du tout... ? J'ai pensé a des sinusoïdes ou des trucs comme ça mais je n'en ai pas vraiment trouvée...

[ThSQ]

Juge par toi même :

http://fr.wikipedia.org/wiki/Espace_complet#Compl.C3.A9t.C3.A9_d.27un_espace_m.C3.A9trique

[quinto]

Ta question est mal posée et finalement c'est de là que viens ton interrogation.
Tu sais que R* se plonge dans R, mais si tu ne le savais pas, tu n'aurais pas pu dire qu'elle "convergeait".

La complétion et la réponse donnée par mon prédécesseur apportera ce que tu cherches.

Finalement en un sens, la réponse est "non".

[Cyril Mar]

Il me semble qu'il suffit tout simplement de restreindre l'ensemble. Par exemple, une suite de Cauchy qui aurait pour valeur d'adhérence un irrationnel ne serait plus convergente (forcément) dans Q. Mais je n'ai jamais réfléchi au fait qu'une suite de Cauchy pouvait être non convergente dans R.

[Joker62]

Au final pour résumer : une suite de Cauchy qui ne converge pas, convergera forcément dans un espace plus grand que celui initial et qui s'apelle le complété...
R est le complété de Q par exemple :)
Juste pour info : la preuve est moche :D

[ffpower]

La preuve n est pas tres compliquée et plutot intuitive :pour compléter un espace (X,d),l idée c est juste que chaque suite de Cauchy converge qque part.Pour chaque suite de Cauhy u=(u_n) de X ne convergeant pas dans X,on rajoute a X un element abstrait l(u) correspond intuitivement a la limite de u_n.Le petit probleme si on a une autre suite v=(v_n) telles que d(u_n,v_n) tend vers 0,u et v doivent avoir meme limite,donc faut juste faire gaffe que dans ce cas on doit prendre l(v)=l(u).Une fois qu on ajouté ces éléments,on obtient un nouvel ensemble Y contenant X.On prolonge notre métrique sur Y on posant d(l,l')=lim d(x_n,y_n) ou (x_n) ,(y_n) sont des suites de X "censées" converger respectivement vers l et l',et c est bon on a notre complété(c est pas dur de montrer que Y est complet).Faut juste ecrire le tout p-e un chouia plus mathematiquement et verifier 2 3 détails,mais bon l idee principale c est ca en tout cas.

[skilveg]

Pour une suite de Cauchy qui diverge vraiment (enfin, qui ne converge pas dans le complété), on peut prendre dans muni de la norme infinie. En général, la dimension infinie apporte pas mal de contre-exemples...

[ffpower]

Je ne comprend pas ce que tu veux dire,ca existe pas une suite de Cauchy qui "diverge" vraiment.Et j ai pas compris ton exemple,c la norme infinie sur quoi?[-1,1]?

[ThSQ]

Une suite de Cauchy qui ne converge pas dans le complété, ça m'interpelle grave au niveau de mon moi topologique !

Tu peux nous dire explicitement quelle norme tu utilises sur IR[X] (la norme infinie = max_IR |P(x)| n'existe évidemment pas) ?

Tu restreins donc probablement le max à un intervalle (style I=[0;1]) mézalor le complété de IR[X] muni de max_I |P(x)| "est" C°(I) muni de la norme infinie qui est complet et la limite de ta suite est 0, donc tout est sauf.


Edit : je vois que ffpower a les mêmes interrogations

[skilveg]

C'était une façon de parler. La norme infinie sur 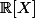en général c'est le sup des valeurs absolues des coefficients, mais la norme infinie sur ça marcherait aussi.

Edit: en effet c'est n'importe quoi de dire qu'elle ne converge pas dans le complété... Ce que je voulais dire c'est que ce n'est pas qu'une variante d'une suite convergente, pour laquelle on aurait enlevé la limite à l'espace ambiant.

Enfin, je voulais juste répondre à la question de départ, quoi...

[ffpower]

Pour les 2 normes que tu cites,ta suite tend vers 0 non?

[skilveg]

Effectivement, la prochaine fois je réfléchirai... Je pensais à qui cette fois-ci converge dans mais pas dans .

Bref...

[ffpower]

ok lol.Mais du coup la encore,c est un exemple ou on "sent" que ca converge qque part meme sans connaitre les complétés d espaces.Un exemple de suite de Cauchy suffisament tordue pour qu on ne voie pas du tout ce que peut bien représenter la limite doit etre chaud a trouver je pense^^

[leon1789]

Au final pour résumer : une suite de Cauchy qui ne converge pas, convergera forcément dans un espace plus grand que celui initial et qui s'apelle le complété...
R est le complété de Q par exemple
Juste pour info : la preuve est moche

La preuve de quoi ? Que R est le complété de Q ? Mais on peut prendre ça comme définition de R, non ?!

oups, désolé, j'ai deux métros de retard.... :help:

[leon1789]

Effectivement, la prochaine fois je réfléchirai... Je pensais à qui cette fois-ci converge dans mais pas dans .

Bref...

oui, des espaces incomplets, il y a en a à la pelle

[Cyril Mar]

Peut-être qu'en définissant une suite de Cauchy à partir d'une fonction par morceaux on peut trouver une suite de Cauchy non convergente sur R.

[leon1789]

une fonction par morceaux ? une suite de Cauchy non convergente sur R ??

[emdro]

Bonjour,

en résumé, une suite de Cauchy, c'est une suite qui a le comportement d'une suite convergente, c'est à dire qu'elle se "stabilise".

L'intuition est que dans ce cas, il y aura une valeur L dont on se rapproche. Dans ce cas la suite est convergente.

Mais parfois, la suite se stabilise autour d'un "trou". Par exemple, pour un individu ne connaissant que les rationnels, donnons l'exemple d'une suite rationnelle qui converge vers un irrationnel. Et c'est en compétant ces trous qu'on définit un espace plus grand, où cette même suite convergera.