Structure d'anneau
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 05 Déc 2021, 17:11
par ComeDuRondeau » 05 Déc 2021, 17:11
Hello,
Je me demandais s'il existait plusieurs classes d'isomorphisme d'anneaux ayant pour groupe additif sous-jacent isomorphe à
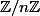
. Intuitivement, je dirais qu'il n'y a qu'une seule classe mais je n'arrive pas à le montrer.
Vous avez des idées ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2021, 18:22
par Ben314 » 05 Déc 2021, 18:22
Salut,
J'ai pas encore réfléchi à la question, mais ça risque de dépendre de ce que tu met dans la définition d'anneau :
- Forcément commutatif ?
- Forcément unitaire ?
(si je dit ça, ça vient aussi du fait qu'en fonction du contexte, on prend pas toujours la même définition de ce qu'est un anneau)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 09 Déc 2021, 12:05
par ComeDuRondeau » 09 Déc 2021, 12:05
Ah oui oui oui pardon, commutatif et unitaire. Même avec ces deux hypothèse, je n'ai pas réussi à m'en tirer. Avec le morphisme caractéristique
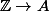
j'obtiens que

admet un sous anneau isomorphe à
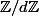
avec
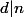
mais même comme ça je m'en sors pas.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Déc 2021, 18:27
par Ben314 » 09 Déc 2021, 18:27
Pour commutatif unitaire, il n'y a qu'une seule structure multiplication à isomorphisme près :
Notons * la "nouvelle" multiplication, e son neutre.
Cherchons l'ordre additif de e : soit k un entier naturel tel que e+e+...+e=0 (k fois e). On a donc (e+e+...+e)*1=0*1=0 puis en distribuant et du fait que e*1=1 on obtient 1+1+...+1=0 ce qui signifie que k est multiple de n. Donc l'ordre additif de e c'est n et ça signifie que e est inversible pour la multiplication usuelle : soit d son inverse (pour le produit usuel). Si on prend maintenant deux éléments quelconques x et y de Z/nZ et qu'on considére des entiers naturels p et q tels que classe(p)=dx et classe(q)=dy on a x=classe(p)e=e+e...+e (p fois) et, de même, y=e+e+...+e (q fois) donc en développant x*y et compte tenu du fait que e*e=e, on a
x*y=e+e+...+e (pq fois) c'est à dire
x*y=classe(pq)e=(dx)(dy)e=dxy.
Et si on note f l'automorphisme additif de Z/nZ défini par x->dx alors on a f(x*y)=f(x)f(y) ce qui prouve que les deux structures sont isomorphe (et en fait on peut prendre comme neutre du nouveau produit n'importe quel élément inversible pour le produit usuel)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 09 Déc 2021, 20:05
par ComeDuRondeau » 09 Déc 2021, 20:05
Ben314 a écrit: On a donc (e+e+...+e)*1=0*1=0 puis en distribuant et du fait que e*1=1 on obtient 1+1+...+1=0 ce qui signifie que k est multiple de n.
Très habile ! On peut en fait s'arrêter là ! Ça nous dit que la caractéristique de

est

donc que le noyau de
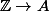
est l'idéal
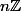
donc par le théorème d'isomorphisme on a

qui contient un sous-anneau isomorphe à
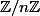
qui est

par égalité des ordres.
Merci Ben

!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités