Bonjour à tous.
Exercice:
Soit n un entier naturel non nul. Montrer qu’il n’existe pas de ra-
tionnels x et y tels que x+y +1/x +1/y=3n
Structure Algébrique
10 messages
- Page 1 sur 1
Re: Structure Algébrique
Veuillez me répondre svp. Moi j'ai voulu raisonner par l'absurde en posant x=p/q et y=s/t avec p^t=s^t=1.
J'ai transformé l'égalité jusqu'à trouver
(pt+qs)(ps+qt)=3npqst. Je cherche l'absurdité mais je trouve pas.
J'ai transformé l'égalité jusqu'à trouver
(pt+qs)(ps+qt)=3npqst. Je cherche l'absurdité mais je trouve pas.
Re: Structure Algébrique
Bonjour
Le nombre n'est qu'un trop l'oeil car si
n'est qu'un trop l'oeil car si  il n'y pas de solutions réelles >0.
il n'y pas de solutions réelles >0.
Le seul cas à étudier est donc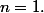
Le nombre
Le seul cas à étudier est donc
Modifié en dernier par aviateur le 27 Jan 2019, 22:58, modifié 1 fois.
Re: Structure Algébrique
Stp j'ai pas encore compris pourquoi pour n\geq2 il n'y a pas de solutions réelles strictement positives
Re: Structure Algébrique
#Aviateur
En posant x=y=\frac{3+\sqrt{5}}{2} j'ai
\frac{1}{x}=\frac{1}{y}=\frac{3-\sqrt{5}}{2} et je trouve x+y+1/x+1/y=3*2. Sauf si j'ai pas compris ce que tu veux dire en disant que n=1.
En posant x=y=\frac{3+\sqrt{5}}{2} j'ai
\frac{1}{x}=\frac{1}{y}=\frac{3-\sqrt{5}}{2} et je trouve x+y+1/x+1/y=3*2. Sauf si j'ai pas compris ce que tu veux dire en disant que n=1.
Re: Structure Algébrique
Rebonjour, Non je me suis trompé il faut dire le contraire:
 pour tout x,y>0. (vient de x+1/x>=2).
pour tout x,y>0. (vient de x+1/x>=2).
Ce qu'il faut dire c'est que pour n=1 il n'y a pas de solution.
Alors c'est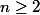 qu'il faut étudier.
qu'il faut étudier.
Ce qu'il faut dire c'est que pour n=1 il n'y a pas de solution.
Alors c'est
Re: Structure Algébrique
ReBonjour
voici une piste à explorer
On pose x+1/x=p/q (irréductible) donc y+1/y=3-p/q.
Donc en calculant x et y en fonction de p et q on voit que nécessairement
 est un carré parfait ainsi que
est un carré parfait ainsi que ^2- 4 q^2)
On a^2) (z,2q,p) est un triplet pythagoricien.
(z,2q,p) est un triplet pythagoricien.
Voir alors les expressions possibles de p et q
Faire de même avec le second carré parfait et voir si les expressions sont compatibles pour trouver des solutions ou non.
voici une piste à explorer
On pose x+1/x=p/q (irréductible) donc y+1/y=3-p/q.
Donc en calculant x et y en fonction de p et q on voit que nécessairement
On a
Voir alors les expressions possibles de p et q
Faire de même avec le second carré parfait et voir si les expressions sont compatibles pour trouver des solutions ou non.
Modifié en dernier par aviateur le 28 Jan 2019, 11:21, modifié 1 fois.
Re: Structure Algébrique
Rebonjour
Sinon on peut faire comme ceci:
posons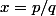 et
et 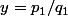 fractions irréductibles
fractions irréductibles
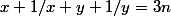 est équivalent à
est équivalent à
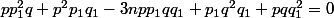
ou encore
à
=p q (3 np_1q_1-p_1^2-q_1^2))
Soit a un diviseur premier de p (resp de q) , il ne peut diviser sinon il diviserait
sinon il diviserait 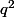 donc q.
donc q.
Donc a divise (idem pour q).
(idem pour q).
De façon analogue un diviseur de ou de
ou de 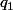 va diviser p q.
va diviser p q.
Autrement dit on a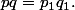
La dernière équation devient donc
=3 n p_1 q_1 - p_1^2 -q_1 ^2)
ou encore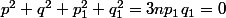 mod (3)
mod (3)
On étudie chaque cas possibles (mod 3).
Supposons que p=0. Alors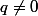 (car p et q premiers entre eux)
(car p et q premiers entre eux)
Mais alors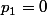 ou exclusif
ou exclusif 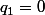 mais alors on a une somme de 2carrés de nombre non nuls égal à 0 et c'est impossible.
mais alors on a une somme de 2carrés de nombre non nuls égal à 0 et c'est impossible.
Pour des raisons de symétries on en déduit que
Supposons p= q=1 alors soit p_1=q_1=1 soit p_1=q_1=2.
Dans tous les cas mod (3)
mod (3)
Supposons alors par exemple
alors par exemple 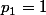 et
et 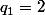 mais encore une fois
mais encore une fois
 mod (3)
mod (3)
Les autres cas étant des cas "symétriques" on a fini. Il n'y a aucune solution.
Sinon on peut faire comme ceci:
posons
ou encore
à
Soit a un diviseur premier de p (resp de q) , il ne peut diviser
Donc a divise
De façon analogue un diviseur de
Autrement dit on a
La dernière équation devient donc
ou encore
On étudie chaque cas possibles (mod 3).
Supposons que p=0. Alors
Mais alors
Pour des raisons de symétries on en déduit que
Supposons p= q=1 alors soit p_1=q_1=1 soit p_1=q_1=2.
Dans tous les cas
Supposons
Les autres cas étant des cas "symétriques" on a fini. Il n'y a aucune solution.
Modifié en dernier par aviateur le 29 Jan 2019, 10:13, modifié 1 fois.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
