Sous groupe et sous groupe engendré

[MC91]

Bonsoir,

J'aurai voulu savoir pourquoi Gr(ensemble vide)= ensemble contenant e. Je n'arrive pas à determiner les sous groupes contenant l'ensemble vide... En fait ce serait les sous groupes qui contiennent 0 élément, mais un sous groupe contient au minimum l'élément neutre???

Autre question, pour démontrer qu'un ensemble H est un sous groupe de G, on doit démontrer que le symétrique de tout élément de H est encore dans H. Par contre on a pas besoin de le démontrer pour justifier qu'un ensemble soit un sous espace vectoriel... Pourquoi donc?

Merci de votre aide.

[vincentroumezy]

Salut.
Le sous-groupe engendré par le vide est le plus petit groupe qui le ontient, et comme un groupe a eau moins un élément, e, c'est forcément {e}.
Ce n'est pas dans le critère des sev, parcque, je pense, c'est impliqué par les propriétés qu'on démontre.

[Nightmare]

Je n'arrive pas à determiner les sous groupes contenant l'ensemble vide...

Es-tu sûr de ta phrase? N'importe quel groupe, et plus généralement n'importe quel ensemble, contient l'ensemble vide!

[MC91]

Oui, exact. J'étais restée sur l'idée que les groupes contiennent au moins un élement et que l'ensemble vide, non. Je me suis un peu embrouillée...

Ok, j'ai compris pour les sous groupes engendrés ! Merci !

[MC91]

Ce n'est pas dans le critère des sev, parcque, je pense, c'est impliqué par les propriétés qu'on démontre.

Je ne vois pas laquelle....

Pour moi, la seule propriété qui pourrait démontrer que le symétrique est dans l'ensemble, c'est celle de la stabilité par addition, mais je ne vois pas trop comment...

[alm]

Salut

Je ne vois pas laquelle....

Soit un espace vectriel et une partie de
est un sous-espace vectoriel de si et seulement si :



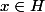
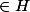
Soit tu veux prouver que ; il suffit d'appliquer pour le couple et et

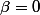
[MC91]

Salut

Soit un espace vectriel et une partie de
est un sous-espace vectoriel de si et seulement si :



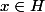
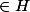
Soit tu veux prouver que ; il suffit d'appliquer pour le couple et et

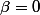
Ah c'est super, merci beaucoup de m'avoir éclairer sur ce point !
Bonne soirée !