Sous groupe engendré par un élément.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
par Aldebaran » 18 Aoû 2005, 16:22
Bonjour à tous ! (heureusement que vous êtes là en ce moment...)
J'ai un petit souci dans la compréhension d'un cours (encore une fois d'algèbre pour ceux qui me connaissent !).
Voilà :
Soit
)
un groupe, de neutre
. Soit
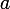
un élément de
.
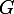
Il est clair que l'application
définie par
=a^m)
est un morphisme de
)
dans
, ( en effet
 \in Z^2, f(m+n)=a^{m+n}=a^m \ast a^n=f(m) \ast f(n))
), et l'image de
n'est autre que le sous-groupe
)
de
engendré par
.
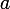
Là où je ne pige plus, c'est quand on dit qu'il existe un unique entier naturel 
tel que  = nZ)
.Quelqu'un pourrait-il bien m'expliquer ce que veut dire cette proposition ?
(je tiens à préciser que j'ai déjà plus ou moins compris cette notion de noyau dans un groupe)...
-
RadarX
- Membre Relatif
- Messages: 333
- Enregistré le: 24 Juil 2005, 19:39
-
par RadarX » 18 Aoû 2005, 16:32
Le ker d'un morphisme f: G -----> H de groupes est un sous groupe de G. C'est relativement facile a verifier.
Donc pour le cas ou G = Z, ker f est un sous groupe de Z; or on sait que les sous groupes de Z sont les ensembles de la forme nZ n>=0. Donc kerf est de la forme nZ! c'est tout.
Par contre si tu n'es pas convaincu qu'un sous groupe de Z est de la forme nZ, tu auras la peuvre dans toute litterature sur les groupes et on y utilise la divison euclidienne dans Z.
RadarX.
-
Aldebaran
- Membre Naturel
- Messages: 41
- Enregistré le: 03 Aoû 2005, 11:36
-
par Aldebaran » 19 Aoû 2005, 09:21
:we: Merci RadarX, c'était pourtant si simple... :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
