Sous groupe engendré

[Anonyme]

bonjour/bonsoir

je pioche de temps en temps des exercices, en voici un :

soient H et K deux sous-groupes d'un groupe G
démontrer :
si HK est un sous-groupe de G
alors HK est le sous-groupe engendré par HUK (noté Gr(HUK))

ma recherche :
comme HK est un sous-groupe de G et comme HUK est contenu dans HK
alors Gr(HUK) C HK
pour l'inclusion inverse, je bloque; pouvez-vous m'aider ?

merci de votre attention

[quinto]

Bonjour.
L'autre inclusion est triviale sauf erreur de ma part, en effet HK est l'ensemble des éléments x de la forme hk h dans H et k dans K.
Notamment HK contient tous les x de la forme h*e où e est le neutre de G, donc tous les x de la forme h dans H, donc HK contient H, et on fait le même raisonnement pour montrer que K est inclus dans HK. On a donc H et K inclus dans HK et donc HUK inclus dans HK.
Sauf erreur de ma part.
A+

[quinto]

Après relecture de la question, j'ai l'impression d'avoir répondu complétement à coté de la plaque....

[Anonyme]

bonjour Quinto

je suis d'accord avec toi :
HK est un sous-groupe de G qui contient HUK
Gr(HUK) étant le plus petit, on a alors :
HUK C Gr(HUK) C HK
mais ça, je l'ai déjà fait; ce que je veux, c'est démontrer que
HK C Gr(HUK)

[Anonyme]

Quinto : "Après relecture de la question, j'ai l'impression d'avoir répondu complétement à coté de la plaque...."

oui, mais tu m'as répondu, et je t'en remercie

[khivapia]

tous les éléments de la forme hk où h est dans H et k dans K sont dans GR(H U K), par stabilité des groupes par la loi interne ! donc HK C Gr(H U K). Ou bien je n'ai rien compris ? :stupid_in :dodo:

[Anonyme]

bonsoir khivapia

je ne te suis pas, pourrais-tu, s'il-te-plaît, éclaircir la chose

je pensais pouvoir utiliser le fait que, comme HK est un sous-groupe de G alors HK=KH, mais cette piste ne me mène nulle part

[quinto]

Khivapia, cette réponse me semble correcte.
En effet, G= donc G contient tous les éléments de H et tous ceux de K, et par stabilité, on a notamment qu'il contient tous les produits possibles entre les éléments de H et de K, notamment il contient HK.
Sauf erreur(s).
A+

[Anonyme]

Et pour quelle raison G=Gr(HUK) ?

Je vais, peut-être, réécrire l'énoncé avec les notations de Quinto :
(conversion : Gr(A) est la même chose que )

Démontrer que :
[center]HK HK = [/center]

[khivapia]

désolé pour le peu de clarté de ma réponse, quinto l'a reformulée plus clairement.


Merci de la confirmation ;)

[quinto]

Ce que j'appelle G c'est , tu peux l'appeler comme ca te chante, mais je n'ai pas fait attention au fait que tu avais un groupe G au départ.
Ce n'est pas le même G qu'au départ.
Désolé de la possible confusion.
A+

[Anonyme]

ha , d'accord ! j'ai eu peur :euh:

bon, alors le truc c'était :
H C HUK C
K C HUK C

< G => HK C

et bien merci à vous deux !

[sept-épées]

pour redire la chose de façon concise :

tout ss-groupe de G qui contient H et K doit contenir HK. Comme HK est un ss-groupe de G, c'est bien le plus petit sous-groupe contenant H et K.

De même, si HKH est un ss-groupe de G, c'est ...et si c'est HKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHKHK qui est un sous-groupe de G, c'est lui ...

:marteau:

[Anonyme]

ne te moquerais-tu pas un peu de moi là ?

[sept-épées]

je ne me permettrais pas!

[sept-épées]

Vous savez ce que c'est que le normalisateur d'un sous-groupe H d'un groupe G? pour ceux qui ne savent pas : c'est l'ensemble des x de G tels que xHx-1 = H, autrement dit c'est le plus grand sous-groupe de G contenant H dans lequel H soit distingué.

petite question :

montrez que si H est un sous-groupe d'un groupe G, N son normalisateur, et K un sous-groupe de N, alors KH est un groupe et H est distingué dans KH.

Etant donnés deux ss-gr H et K de G, vous avez sous la main une condition nécessaire et suffisante pour que KH soit un groupe...

[Anonyme]

bonjour sept-épées

*
pour montrer que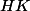 est un groupe, on peut montrer que c'est un sous-groupe de
pour cela, on peut démontrer que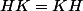
prenons
comme alors
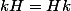
en particulier, il existe un tel que
ce qui montre que
par suite,
on fait de même pour montrer l'inclusion inverse

**
pour montrer que est un sous-groupe normal de , on peut montrer que (après avoir montré que )
pour tout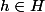 , et pour tout ,

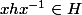
soit alors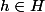 un et un
on sait que (puisque )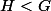
or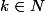 (puisque )
en particulier,

[sept-épées]

Pour la première question, relis-toi. Tu as l'air de montrer que HK est un ss-groupe de G sans utiliser l'hypothèse K
En revanche, il est vrai que HK est un sous-groupe de G ssi HK=KH.

Pour la deuxième question, c'est exactement ça.
(On peut juste s'épargner quelques notations en écrivant :

khHh-1k-1 = kHk-1 C kHK = kKH =KH )

(désolé pour ce truc illisible, je veux bien que qqn m'explique comment utiliser TEX )

[Crayon Volant]

bonsoir sept-épées ( et merci pour ton attention )

Je la refais :

correction avec les *

prenons
* comme alors
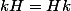
en particulier, il existe un tel que
ce qui montre que
** par suite,
on fait de même pour montrer l'inclusion inverse

c'est que j'ai mal recopié mon brouillon en *
et en ** c'est que j'ai mal relu


pour tex : tu/vous mets/mettez ton/votre code entre les balise [ tex] et [ /tex]
(sans les espaces)
les accolades ont valeur de groupe : par exemple :
[ tex] h^{123}[ /tex] donne
alors que
[ tex]h^123[ /tex] donne
pour l'inclusion , c'est la macro \subset :
[ tex]A\subset B[/tex] donne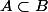
ne pas oublier l'espace après une macro, car la macro \subsetB n'existe pas

[sept-épées]

Je te/vous remercie