Sous-espace dans les matrices

[michal]

Voilà. Je sèche sur l'exo suivant :

Existe-t-il des sous-espaces vectoriels de de dimension trois dont les éléments commutent deux à deux ?

Je suis preneur de toute idée, même si elle n'aboutit pas...

Merci d'avance. :help:

[Zebulon]

Bonjour,
là, il est 8 heures du matin... La première chose qui me passe par la tête, c'estde chercher les conditions nécessaires pour que deux matrices 3X3 commutent.
Si j'ai le temps dans la journée, je chercherai un peu plus. Comme tu as dit que tu étais preneur de toute idée, voilà! :happy2:
Bon courage et à bientôt,
Zeb.

[Zebulon]

En effet, il était 8 heures et on parlait de matrices 2X2, ce qui est déjà mieux!
Soient ,
Quand on multiplie ces deux matrices dans les deux sens et qu'on idetifie, on obtient le système
.
A part que les première et dernière ligne sont identiques, je ne vois pas ce que ça apporte...
Désolée...
Bon courage!

[michal]

J'ai fini par trouver une réponse qui utilise ton calcul :
Si , alors si on pose (commutant de ), alors :
- Si est scalaire, ;
- Si n'est pas scalaire, ;
En effet le premier cas est évident et dans le deuxième :
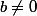
- soit et alors g et e s'expriment en fonction de f et h
- soit et alors f et g s'expriment en fonction de e et h
- soit et ...
On peut alors conclure que l'espace cherché n'existe pas.