Bonjour,
J’ai un devoir à rendre et depuis quelques jours je bloque totalement sur cet exercice.
Soit n e N*, Vérifier que :
∑(avec k allant de 1 à n) k2^k = ∑(k allant de 1 à n) ∑(allant de l=1 à k) 2^k
En déduire la valeur de la somme.
Je bloque totalement, j’ai essayé de chercher avec mes formules du cours (reconnaître une suite géométrique, changement d’indice...) mais je ne trouve aucun raisonnement qui aboutisse.
Merci beaucoup,
Somme
6 messages
- Page 1 sur 1
Re: Somme
GaBuZoMeu a écrit:Bonjour,
As-tu pensé à intervertir les deux sommations ( celle suret celle sur
) ?
J’ai justifié la première question en expliquant que 2^k était indépendant de l, et donc qu’on trouvait ∑(k-1+1).2^k et donc ∑2^k
Pour la suite, j’ai essayé en utilisant la formule de la somme géométrique combinée à la somme triangulaire. Je trouve en résultat (n-1)^(2n+1)+2
Re: Somme
Ta formule ne marche pas pour n=2 (toujours penser à vérifier sur des petits entiers quand on pense avoir trouvé une expression de la somme).
Je renouvelle ma suggestion : intervertir les sommations pour faire :
somme pour l allant de 1 à n de somme pour k allant de ? à ? ....
Je renouvelle ma suggestion : intervertir les sommations pour faire :
somme pour l allant de 1 à n de somme pour k allant de ? à ? ....
Re: Somme
GaBuZoMeu a écrit:Ta formule ne marche pas pour n=2 (toujours penser à vérifier sur des petits entiers quand on pense avoir trouvé une expression de la somme).
Je renouvelle ma suggestion : intervertir les sommations pour faire :
somme pour l allant de 1 à n de somme pour k allant de ? à ? ....
Bonsoir,
Je ne comprends pas comment faire pour intervenir les sommations et les indices comme vous le dites,
Merci
Re: Somme
On fait la somme sur tous les couples ) avec
avec  .
.
Imagine un tableau avec comme indice de ligne et
comme indice de ligne et  comme indice de colonne, en mettant
comme indice de colonne, en mettant 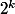 dans chaque case
dans chaque case ) avec
avec 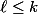 .
.
La somme qui est écrite est une somme par ligne (on fixe d'abord ).
).
On obtient le même résultat en faisant une somme par colonne (on fixe d'abord )
)
Imagine un tableau avec
La somme qui est écrite est une somme par ligne (on fixe d'abord
On obtient le même résultat en faisant une somme par colonne (on fixe d'abord
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
