Somme
25 messages
- Page 1 sur 2 - 1, 2
somme
Bonjour :
Je dois calculer la somme S1= Somme des k=0 jusqu'à n pour k pair ne (k parmi n)2k puis S2= la même somme que S1 pour les k impairs.
Je dois d'abord calculer S1+S2 puis S1-S2 et donc ensuite grâce à un système, trouver S1 et S2.
Cependant, ce sont les pairs et impairs qui me gènent pour écrire les relations de Newton.
Pouvez vous m'expliquer ? merci
Je dois calculer la somme S1= Somme des k=0 jusqu'à n pour k pair ne (k parmi n)2k puis S2= la même somme que S1 pour les k impairs.
Je dois d'abord calculer S1+S2 puis S1-S2 et donc ensuite grâce à un système, trouver S1 et S2.
Cependant, ce sont les pairs et impairs qui me gènent pour écrire les relations de Newton.
Pouvez vous m'expliquer ? merci
Le calcul de S1+S2 ne demande pas de savoir distinguer les pairs des impairs vu... qu'on ajoute tout le monde...
Pour le calcul de S1-S2, une "indication" :
pour distinguer k pair de k impair, il suffit de calculer (-1)^k qui vaut +1 si k est pair et -1 s'il est impair.
Pour le calcul de S1-S2, une "indication" :
pour distinguer k pair de k impair, il suffit de calculer (-1)^k qui vaut +1 si k est pair et -1 s'il est impair.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Dans le binôme de newton, il apparait des a^k.b^(n-k) derrière les coeff. binomiaux.
Dans le cas de S1+S2, tu voudrait que tout ces a^k.b^(n-k) valent 1 pour avoir la somme sans coeff. : il y a une solution simple a=... ; b= ...
Dans le cas de S1-S2, tu voudrait que les a^k.b^(n-k) valent 1 ou -1 selon que k est par ou impair : c'est à peine plus compliqué a=... ; b=...
P.S. Non, en fait, c'est un peu plus compliqué que ce que je pensait (j'avais pas fait gaffe au 2k
Dans le cas de S1+S2, tu voudrait que tout ces a^k.b^(n-k) valent 1 pour avoir la somme sans coeff. : il y a une solution simple a=... ; b= ...
Dans le cas de S1-S2, tu voudrait que les a^k.b^(n-k) valent 1 ou -1 selon que k est par ou impair : c'est à peine plus compliqué a=... ; b=...
P.S. Non, en fait, c'est un peu plus compliqué que ce que je pensait (j'avais pas fait gaffe au 2k
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, mais en fait c'est un peu plus compliqué que ce que je pensait à cause du 2k devant le coeff binomial.
N'empèche que ça permet quand même d'écrire que

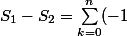^k 2k{n\choose k})
Maintenant, le problème, c'est d'arriver à enlever le "2k" (voire juste le k vu que le 2 on peut le faire passer devant le sigma).
As tu déjà rencontré ce type de sommes ? (Il y a au moins 2 méthodes pour s'en sortir)
N'empèche que ça permet quand même d'écrire que
Maintenant, le problème, c'est d'arriver à enlever le "2k" (voire juste le k vu que le 2 on peut le faire passer devant le sigma).
As tu déjà rencontré ce type de sommes ? (Il y a au moins 2 méthodes pour s'en sortir)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
d'accord mais juste une précision :
quand vous écrivez S1+S2 ça donne un résultat pair non ? pourquoi ? et pour quoi S1-S2 donne un impair? ça rejoint à ce que vous m'avez expliquez dans le message précédent mais j'ai du mal à comprendre pourquoi...
autrement :
si je soustrais les deux membres ça donne : 2S2=?
quand vous écrivez S1+S2 ça donne un résultat pair non ? pourquoi ? et pour quoi S1-S2 donne un impair? ça rejoint à ce que vous m'avez expliquez dans le message précédent mais j'ai du mal à comprendre pourquoi...
autrement :
si je soustrais les deux membres ça donne : 2S2=?
Sinon, les deux méthodes pour calculer 
c'est :
Méthode 1 : pour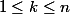 (mais pas pour k=0) on a :
(mais pas pour k=0) on a :
!}\;=\;\frac{n!}{(k-1)! (n-k)!}\;<br />=\;n\frac{(n-1)!}{(k-1)! (n-k)!}\;=\;n{n -1\choose k-1})
et le "n" n'est pas gênant : dans la somme c'est une constante donc on peut le "sortir" du sigma.
Méthode 2 :
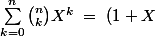^n)
Si je dérive des deux cotés (par rapport à X) puis que je prend X=1, jobtiens...
Et on fait (quasi) la même chose pour S1-S2.
c'est :
Méthode 1 : pour
et le "n" n'est pas gênant : dans la somme c'est une constante donc on peut le "sortir" du sigma.
Méthode 2 :
Si je dérive des deux cotés (par rapport à X) puis que je prend X=1, jobtiens...
Et on fait (quasi) la même chose pour S1-S2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
ok
Maintenant, le problème, c'est d'arriver à enlever le "2k" (voire juste le k vu que le 2 on peut le faire passer devant le sigma).
As tu déjà rencontré ce type de sommes ? (Il y a au moins 2 méthodes pour s'en sortir)
pour S1+S2, je mets le 2 devant et du coup je trouve comme résultat final : 2n2^(n-1) par contre pour S1-S2 je ne sais pas trop faire
Maintenant, le problème, c'est d'arriver à enlever le "2k" (voire juste le k vu que le 2 on peut le faire passer devant le sigma).
As tu déjà rencontré ce type de sommes ? (Il y a au moins 2 méthodes pour s'en sortir)
pour S1+S2, je mets le 2 devant et du coup je trouve comme résultat final : 2n2^(n-1) par contre pour S1-S2 je ne sais pas trop faire
pluie2 a écrit:pour S1+S2, je mets le 2 devant et du coup je trouve comme résultat final : 2n2^(n-1) par contre pour S1-S2 je ne sais pas trop faire
C'est O.K. pour S1+S2.
Comment a-tu fait pour le trouver ? (normalement avec une méthode très semblable tu devrait trouver S1-S2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
pluie2 a écrit:j'ai fait : 0*(0 parmi n) + somme de k=1 à n de k*(k parmi n)= somme de k=1 à n de n*(k-1 parmi n-1)= n * somme de k=1 à n de (k-1 parmi n-1). Changement d'indice j=k-1 donc ça donne : n* somme de j=0 à n-1 de (j parmi n-1)= n(1+1)^(n-1)
oui mais pour S1-S2 je ne sais pas quoi faire du (*1)^k
Dans ta preuve, à la fin, tu utilise le fait que "somme de j=0 à n-1 de (j parmi n-1)= (1+1)^(n-1)"
C'est le binôme de newton avec a=b=1.
Et avec a=-1, b=1, ça dit quoi le binôme de newton ? y'aurais pas justement des (-1)^k qui apparaissent ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
