Somme "générale" des carrés d'entiers

[Yann_Benoit]

Bonjour,

Lorsqu'on fait la somme d'entiers allant de 1 à n (n fini), on a la formule standard n(n+1)/2, formule qui peut se "généraliser" par l'expression, lorsque la suite (finie) ne commence pas par l'entier 1 : "(nombre de termes) x (moyenne des extrêmes)".

Existe-t-il une formule similaire "générale" pour une suite (finie) de carrés d'entiers, le premier entier n'étant pas égal à 1 ?

Merci !

[Archibald]

[Yann_Benoit]

Merci Archibald. Je connaissais la formule et il n'y a donc pas d'équivalent "littéraire" général lorsque le premier terme dans le sigma n'est pas égal à 1 (et qu'on connaît le dernier terme), comme on peut le faire pour la somme de n premiers termes commençant par 1 ?
Merci.

[Monsieur23]

Aloha,

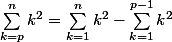
Tu peux utiliser le fait que, et tu te ramènes donc à deux sommes que tu sais calculer… En soustrayant, tu auras ta formule.

[Yann_Benoit]

Merci beaucoup Monsieur23 ! C'est ce que je cherchais... et c'est si simple (quelle honte ! :ptdr:) !