salut,
j'ai une question
pour determiner que G=F(+)H est ce il suffit de demontrer que dimG=dimF+dimH
*avec (+) est une somme directe
mercie d'avance
Somme directe
6 messages
- Page 1 sur 1
Pour toutes ces histoires de sommes directes, il n'y a qu'une seule chose à savoir : la définition !
Soit_{i\in I}) , avec I fini ici, une famille de s.e.v de E.
, avec I fini ici, une famille de s.e.v de E.
On considère l'application linéaire_i\in\prod_{i\in I} F_i \to \sum_i x_i \in E) . On définit
. On définit 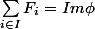 .
.
On dit que les sont en somme directe si l'application
sont en somme directe si l'application  est injective.
est injective.
A partir de là, le cas de la dimension finie est simple : il suffit d'appliquer le théorème du rang.
Soit
On considère l'application linéaire
On dit que les
A partir de là, le cas de la dimension finie est simple : il suffit d'appliquer le théorème du rang.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
