Somme directe
19 messages
- Page 1 sur 1
somme directe
Bonsoir , j'ai l'exercice suivant :
Soit f un endomorphisme dun espace vectoriel E sur un corps commu-
tatif k. Posons
F = Ker(f ;) id) = {x ;) E | f(x) = x}.
Montrer que la somme F + Ker(f) est directe.
Ma réponse : on sait que pour qu'une somme soit directe il faut que l'intersection des 2 espaces soit réduite au vecteur nul .
Supposons que F et ker(f) = {0} .
Soit u un élément de F et ker(f) .
u = x + v
u = x' + v'
En fait là j'essaye d'utiliser la démonstration du théorème mais je n'y arrive pas car je sais pas comment traduire un élément de ker(f)..
quelqu'un aurait il une idée ?
merci
Soit f un endomorphisme dun espace vectoriel E sur un corps commu-
tatif k. Posons
F = Ker(f ;) id) = {x ;) E | f(x) = x}.
Montrer que la somme F + Ker(f) est directe.
Ma réponse : on sait que pour qu'une somme soit directe il faut que l'intersection des 2 espaces soit réduite au vecteur nul .
Supposons que F et ker(f) = {0} .
Soit u un élément de F et ker(f) .
u = x + v
u = x' + v'
En fait là j'essaye d'utiliser la démonstration du théorème mais je n'y arrive pas car je sais pas comment traduire un élément de ker(f)..
quelqu'un aurait il une idée ?
merci
Bon il faut montrer que \cap ker(f-Id)=\{0\})
C'est à dire qu'il faut montrer que si on prend un élément commun à Ker(f) et ker(f-Id) alors il est forcément nul.
Soit x un élément appartenant aux deux.
Comme il appartient à Ker(f), f(x)=0
de plus comme il appartient à Ker(f-Id), f(x)=x
Mais si f(x)=0 et f(x)=x alors x=0.
Ainsi tout élément appartenant aux deux ensembles est nul.
L'intersection est deux est donc réduite à {0}. Ils sont donc par définition en somme directe.
C'est à dire qu'il faut montrer que si on prend un élément commun à Ker(f) et ker(f-Id) alors il est forcément nul.
Soit x un élément appartenant aux deux.
Comme il appartient à Ker(f), f(x)=0
de plus comme il appartient à Ker(f-Id), f(x)=x
Mais si f(x)=0 et f(x)=x alors x=0.
Ainsi tout élément appartenant aux deux ensembles est nul.
L'intersection est deux est donc réduite à {0}. Ils sont donc par définition en somme directe.
là c'est bcp plus clair je te remercie :) , meme si je sais que vos réponses sont toujours bonnes , parfois vous expliquez peu par des phrases , c'est plus difficile à comprendre .
Une derniere petite question si ça te gene pas : si on suppose que f o f = f et qu'on demande de montrer que la somme directe de F et kerf = E , comment tu ferais ?
je suppose que le f o f caracterise un endomorphisme ou alors que le f o f a un rapport avec le corps commutatif k non ?
Une derniere petite question si ça te gene pas : si on suppose que f o f = f et qu'on demande de montrer que la somme directe de F et kerf = E , comment tu ferais ?
je suppose que le f o f caracterise un endomorphisme ou alors que le f o f a un rapport avec le corps commutatif k non ?
Si je n'ai pas fait de phrases c'est parce que tout ceci est d'un niveau très simple, tu dis ne pas être bonne en maths mais pour faire des exercices sur les endomorphismes d'espaces vectoriel c'est que tu as choisi une voie du supérieure où l'on fait des maths à bon niveau, pourquoi ce choix si tu n'es pas douée en maths?
Soit x un élément de E.
Alors x=f(x)+(x-f(x))
Montrons que f(x) est dans Ker(f-Id) et que x-f(x) est dans Ker(f)
(f-Id)(f(x))=fof(x)-f(x)=f(x)-f(x)=0 d'où f(x) est dans ker(f-Id)
f(x-f(x))=f(x)-fof(x)=f(x)-f(x)=0 donc x-f(x) est dans Ker(f)
Au final tout vecteur de E s'écrit comme une somme d'éléments de Ker(f) et de Ker(f-Id) ie : E=Ker(f)+Ker(f-Id)
Alors x=f(x)+(x-f(x))
Montrons que f(x) est dans Ker(f-Id) et que x-f(x) est dans Ker(f)
(f-Id)(f(x))=fof(x)-f(x)=f(x)-f(x)=0 d'où f(x) est dans ker(f-Id)
f(x-f(x))=f(x)-fof(x)=f(x)-f(x)=0 donc x-f(x) est dans Ker(f)
Au final tout vecteur de E s'écrit comme une somme d'éléments de Ker(f) et de Ker(f-Id) ie : E=Ker(f)+Ker(f-Id)
j'ai pas compris ta démonstration mais bon je ne vais pas te déranger plus longtemps , je vais essayer de comprendre moi meme , si tu pouvais juste me dire ce que c'est ce x=f(x)+(x-f(x)) , surtout ce x-f(x) correspond à quoi , car si dans l'énoncé ils parlent de id et de corps commutatif il doit bien yavoir un rapport avec tes réponses mais je ne les vois guère :triste:
merci pour tout en tout cas .
merci pour tout en tout cas .
C'est vraiment la base... Il faut que tu revoies le cours sur les applications linéaires, les noyaux etc...
J'explique en détail une dernière fois puis après dodo :
On veut montrer que Ker(f)+Ker(f-Id)=E
Qu'est-ce que ça veut dire? Cela veut dire que tout élément de E peut s'écrire comme une somme d'un élément de Ker(f) et d'un élément de Ker(f-Id).
Ma démonstration. On pose x un élément de E. On veut l'écrire comme une somme d'un élément de Ker(f) et d'un élément de Ker(f-Id)
La première chose est d'écrire que x=f(x)+(x-f(x)) (en effet les f(x) se simplifient)
Il reste donc à montrer que f(x) est dans Ker(f-Id) et x-f(x) est dans Ker(f) (cela pourrait être l'inverse, sauf que ça n'est pas le cas et à force de faire des exercices on ne se trompe plus)
Pour montrer que f(x) est dans Ker(f-Id) il faut montrer que l'image de f(x) par f-Id est nulle.
Or (f-Id)(f(x))=fof(x)-Idof(x)
Mais fof(x)=f(x) (posé dans l'énoncé)
et Idof(x)=f(x) par définition de Id.
On a donc fof(x)-Idof(x)=f(x)-f(x)=0
c'est à dire (f-Id)(f(x))=0 . On a bien f(x) qui est dans Ker(f-Id)
Montrons à présent que x-f(x) est dans ker(f), c'est à dire que f[x-f(x)]=0
Puisque f est linéaire, f[x-f(x)]=f(x)-fof(x)
Mais fof(x)=f(x)
d'où f[x-f(x)]=f(x)-f(x)=0
On a bien x-f(x) qui est dans Ker(f)
Au final tout vecteur x de E s'écrit comme la somme d'un élément de Ker(f) ( x-f(x) ) et d'un élément de Ker(f-Id) ( f(x) ), ce qui prouve que Ker(f)+Ker(f-Id)=E. Comme de plus on a prouvé que Ker(f) et Ker(f-Id) étaient en somme directe on peut écrire que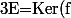\oplus Ker(f-Id))
(Point culturel : Un tel endomorphisme f s'appelle un projecteur)
:happy3:
J'explique en détail une dernière fois puis après dodo :
On veut montrer que Ker(f)+Ker(f-Id)=E
Qu'est-ce que ça veut dire? Cela veut dire que tout élément de E peut s'écrire comme une somme d'un élément de Ker(f) et d'un élément de Ker(f-Id).
Ma démonstration. On pose x un élément de E. On veut l'écrire comme une somme d'un élément de Ker(f) et d'un élément de Ker(f-Id)
La première chose est d'écrire que x=f(x)+(x-f(x)) (en effet les f(x) se simplifient)
Il reste donc à montrer que f(x) est dans Ker(f-Id) et x-f(x) est dans Ker(f) (cela pourrait être l'inverse, sauf que ça n'est pas le cas et à force de faire des exercices on ne se trompe plus)
Pour montrer que f(x) est dans Ker(f-Id) il faut montrer que l'image de f(x) par f-Id est nulle.
Or (f-Id)(f(x))=fof(x)-Idof(x)
Mais fof(x)=f(x) (posé dans l'énoncé)
et Idof(x)=f(x) par définition de Id.
On a donc fof(x)-Idof(x)=f(x)-f(x)=0
c'est à dire (f-Id)(f(x))=0 . On a bien f(x) qui est dans Ker(f-Id)
Montrons à présent que x-f(x) est dans ker(f), c'est à dire que f[x-f(x)]=0
Puisque f est linéaire, f[x-f(x)]=f(x)-fof(x)
Mais fof(x)=f(x)
d'où f[x-f(x)]=f(x)-f(x)=0
On a bien x-f(x) qui est dans Ker(f)
Au final tout vecteur x de E s'écrit comme la somme d'un élément de Ker(f) ( x-f(x) ) et d'un élément de Ker(f-Id) ( f(x) ), ce qui prouve que Ker(f)+Ker(f-Id)=E. Comme de plus on a prouvé que Ker(f) et Ker(f-Id) étaient en somme directe on peut écrire que
(Point culturel : Un tel endomorphisme f s'appelle un projecteur)
:happy3:
Montrer que la somme F + Ker(f) est directe.
Ma réponse : on sait que pour qu'une somme soit directe il faut que l'intersection des 2 espaces soit réduite au vecteur nul.
Supposons que F et ker(f) = {0} .
Petite remarque:
Supposons que F et ker(f) = {0} .
Ta démonstration commence très mal! Comment veux tu prouver que quelque chose est vrai, si tu suppose dès le départ que c'est vrai?
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
