Solution polynôme à coefficients variants

[president13]

bonjour à tous,

je souhaiterais savoir s'il existe des méthodes de résolution de polynômes d'ordre n (ordre 2 pour commencer simple) à coefficients variants (fréquentiellement dans mon cas).
Le résultat étant donc à son tour variant fréquentiellement.

en vous remerciant,

[Nightmare]

Salut,

Plusieurs points vague : Que veut dire "résoudre un polynôme" ? Résoudre une équation je veux bien, trouver les racines d'un polynôme je veux bien, mais "résoudre un polynôme" ??

S'il s'agit de résoudre une équation polynômiale (de degré 2 apparemment), je ne comprends pas trop non plus. Qu'appelles-tu "coefficients variants"? Tu veux dire qu'à la place d'avoir des coefs fixe on a des paramètres? Si c'est le cas ça ne change rien, on applique la formule du discriminant et on exprime les solutions en fonction des paramètres.

Exemple, l'équation x²+tx-1=0 où t est un réel quelconque a pour discriminant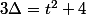 toujours positif. Elle admet donc toujours deux solutions réelles distinctes données par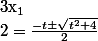

:happy3:

[president13]

bonsoir et merci pour ces premières pistes.

tout d'abord, désolé, je n'ai pas la rigueur mathématique.
pour être plus clair :

je veux effectivement trouver les racines d'un polynôme d'ordre 2.
Les coefficients sont également variants fréquentiellement, car intégrant la variable de Laplace, que l'on notera "s". On les notera respectivement f1(p), f2(p) et f3(p).

l'équation est alors de la forme suivante :

f1(p).X^2 +f2(p).X + f3(p) = 0

En calculant la solution comme dans votre exemple, il apparaît une racine carrée du discriminant qui me pose problème. car les puissances de la variable de Laplace doivent être entières.

est-ce que ça vous paraît plus clair?

merci

[Nightmare]

Re !

Il y a juste ce passage que je ne comprends pas :

car les puissances de la variable de Laplace doivent être entières.

Qu'entends-tu par ici? On a pas le choix de faire apparaitre une racine carrée dans les solutions.

[president13]

oui en effet , pas le choix.

La variable de Laplace est utilisée dans le domaine fréquentiel/complexe.
Par définition, s=jw (j omega, avec J la variable complexe et omega la pulsation.
De plus, lors d'une transformation temporelle vers fréquentielle, la dérivée première dans le temps est exprimée par la variable s. la dérivée seconde par s^2, et ainsi de suite. De même pour les intégrales exprimées par des puissances négatives. mais puissances entières !
La racine carrée vient ici apporter une puissance 1/2, qui n'est pas autorisée dans le monde de Laplace.

Je me demande si je ne pourrais pas m'en tirer avec un développement limité de la fonction racine carrée....je cherche.

encore merci.

[Nightmare]

Ben en fait la "puissance" de p dans les solutions vont dépendre un peu des 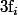. Cela dit, si c'est bien une puissance 1/2 alors faire un DL pour faire apparaitre des puissances entières de p est une bonne idée. Mais encore une fois, comme je ne sais pas ce que tu veux en faire de tout ça, je ne peux rien te dire de plus :happy3:

[president13]

je suis tout à fait d'accord avec vous, les racines vont être fonction des f{i}.

En réalité, j'ai transformé un problème de minimisation en problème de recherche de racines d'un polynôme.

car le vrai problème est le suivant :

f1(p).K^2+f2(p).K=f3(p)

je cherche donc K, pour que | f1(p).K^2+f2(p).K - f3(p) | = 0

encore merci.