Solution "évidente"
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ourfalli
- Membre Naturel
- Messages: 43
- Enregistré le: 09 Aoû 2007, 20:16
-
 par Ourfalli » 25 Oct 2008, 00:51
par Ourfalli » 25 Oct 2008, 00:51
Bonjour,
Après beaucoup d'essais je n'ai pas pu intégrer l'équation
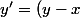^2)
.
En lisant le corrigé, j'ai trouvé que
=x+1)
est une solution évidente, et que pour transformer l'équa.diff. en équation de Bernoulli, il faut poser
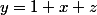
.
Ma question : comment on a "deviné" la superposition de z(x) avec la solution "évidente".
Dans le cours on applique le principe de superposition uniquement avec les équations linéaires de premier ou 2nd ordre, ce n'est pas le cas de l'équation
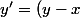^2)
.
Merci pour les astuces.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 25 Oct 2008, 07:07
par Maxmau » 25 Oct 2008, 07:07
Bj
Il est assez naturel ici de poser, dans un premier temps : u(x) = y(x) x
De manière générale, les choses ne paraissent évidentes que dans la mesure où on possède un métier solide en la matière.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 25 Oct 2008, 11:19
par Pythales » 25 Oct 2008, 11:19
L'équation est une équation de Ricatti.
Il est classique pour cette équation, lorsqu'on connait une solution particulière
)
, de poser
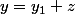
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 25 Oct 2008, 11:50
par _-Gaara-_ » 25 Oct 2008, 11:50
Bernouilli et Ricatti sont des classiques à connaître non ?
-
Ourfalli
- Membre Naturel
- Messages: 43
- Enregistré le: 09 Aoû 2007, 20:16
-
 par Ourfalli » 28 Oct 2008, 01:59
par Ourfalli » 28 Oct 2008, 01:59
Merci,
Effectivement, je suis débutant et autodidacte, donc loin d'avoir un métier solide.
C'est juste un peu de frustration qui m'a pousseé à "oser" pointer mon nez dans le forum.
Je ne connaissait pas le problème de Ricatti, je vais faire des recherches dessus.
J'espère un jour avoir un échange plus intéressant à proposer, d'ici là ...au boulot!
-
Ourfalli
- Membre Naturel
- Messages: 43
- Enregistré le: 09 Aoû 2007, 20:16
-
 par Ourfalli » 28 Oct 2008, 12:50
par Ourfalli » 28 Oct 2008, 12:50
En effet c'est tout bête !
C'est comme une équation de Bernouilli (

) "avec second membre". Si on trouve une solution particulière "par tatônement" il suffit de faire une transormation de variable (et non l'utilisation du principe de superposition) pour éliminer le second membre.
Ainsi :
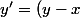^2)
, a visiblement
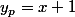
comme SP, donc :

devient par transfomation de variable
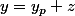
, une eq de Bernouilli.
Avec un peu de métier, la recherche par tatônnement s'améliorera.
Merki.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
