Bonjour ou bonsoir,
On a un espace vectoriel à quatre dimensions et

sous-espace engendré par
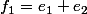
et
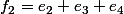
.
On veut :
1- La matrice de projection orthogonale sur

et la matrice de la symétrie orthogonale par rapport à sur

dans la base canonique orthonormée
)
. Pas de problème jusqu'à là.
2 - Une base orthonormale

, dans laquelle la matrice de la symétrie orthogonale par rapport à

est ... "plus simple". Par "plus simple", bien sûr, ça sous-entend la matrice de symétrie
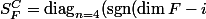))
.
Pour la solution de 1 , je caractérise,
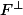
et j'ai les quatre vecteurs dans les colonnes de la matrice :

Pour la symétrie, je trouve :

Pour la question 2, je procède à l'orthogonalisation de Gram-Schmidt pour arriver à :

Cette matrice est bien orthogonale et donc pourrait faire office d'une matrice de passage

telle que :

Et là, j'ai une matrice loin d'être simple.
Je me suis dit que je n'ai pas employé la bonne méthode, où il y a une erreur de raisonnement. J'opte pour trouver une matrice
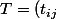)
et trouver un système d'équations pour que son déterminant soit
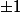
, qui vérifie

. Puis, résoudre une autre système pour vérifier

. Sauf que le calcul est fastidieux.
Je regarde la solution pour trouver cette matrice donnée "par exemple" (sic.) !

Les deux premières colonnes, c'est bien ce que j'ai trouvé. Par contre, le corrigé reprend les deux dernières colonnes de

trouvées par les calculs pour caractériser
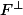
, mais aucune idée comment "on en déduit" les deux derniers vecteurs de

! Ce n'est pas une matrice orthogonale

. Je ne comprends plus rien ! Comment on a trouvé cette matrice ? !!
J'apprécie votre aide, merci d'avance.
