Matrice de symétrie

[Subsib]

Bonjour,

J'ai la solution d'un problème mais ça fait des heures maintenant que j'essaie de comprendre le résultat. J'ai beau essayer de triturer ça dans tous les sens, rien n'y fait.
Est-ce qu'une bonne âme pourrait m'aider ?? :s

Voilà, l'application est une symétrie par rapport à la droite y = 4x.

La solution est une matrice :
-15/17 8/17
8/17 15/17

Je suis affreusement perdue :s

[fatal_error]

hello,

si tu pouvais commencer par nous donner l'énoncé/problème ca pourrait etre un bon début,

parce qu'une solution sans problème c'est pas super..

[Subsib]

hello,

si tu pouvais commencer par nous donner l'énoncé/problème ca pourrait etre un bon début,

parce qu'une solution sans problème c'est pas super..

oui, bien sûr. Sorry, j'suis pas dans mon assiette, j'ai horreur de pas arriver à un truc alors là, je pète un peu les plombs.

L'énoncé, c'est :

"Dans le plan euclidien R2 muni de la base canonique, voici des opérateurs linéaires. Écrivez leur matrice."

Toutes les autres, pas de problème, il s'agit simplement de symétries axiales ou par rapport à l'origine.
Mais là, symétrie par rapport à y = 4x, je comprends pas.

[Sourire_banane]

Salut,

Il faut travailler avec une base convenable, et traiter son problème en termes d'endomorphismes.

Pour R², on peut prendre la base (e1,e2) canonique. Réfléchis maintenant à la manière dont on peut trouver le symétrique de e1 par exemple par rapport à la droite d'équation y=4x.

[Subsib]

Salut,

Il faut travailler avec une base convenable, et traiter son problème en termes d'endomorphismes.

Pour R², on peut prendre la base (e1,e2) canonique. Réfléchis maintenant à la manière dont on peut trouver le symétrique de e1 par exemple par rapport à la droite d'équation y=4x.

un vecteur perpendiculaire à (1, 4) c'est (-4, 1).

Je considère que (1,0) = (,1 4) + ð ( -4, 1)
et que (0, 1) = (1,4) + ð(-4, 1) ?


Je cherche à changer de base, exprimant les vecteurs e'1 et e'2... ?
Quelque chose comme ça...

Je "vois" la symétrie, mais je ne vois pas les calculs qu'il faut poser... :mur:

[Robic]

Est-ce que tu as vu une propriété disant que la matrice d'une symétrie est toujours de la forme

où est lié à la droite par rapport à laquelle on définit la symétrie ?

Si oui, il y a juste à calculer cet angle.

Si non, il y a la méthode habituelle :

Soit M(x,y) un point quelconque du plan. M'(x',y') est son symétrique par rapport à la droite D d'équation y=4x si on a :
(1) le vecteur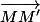 est perpendiculaire à D ;
(2) est colinéaire à un vecteur directeur de D.
(Ça se voit en faisant un dessin.)

(1) et (2) fournissent deux équations dont les inconnues sont x' et y', qu'on exprime en fonction de x et y, ce qui permettra d'obtenir la matrice. ((2) donne a priori deux équations, mais on peut n'avoir qu'une équation en exprimant la colinéarité par un produit en croix.) En procédant ainsi, j'ai retrouvé la matrice annoncée dans le premier message.

[Subsib]

Est-ce que tu as vu une propriété disant que la matrice d'une symétrie est toujours de la forme

où est lié à la droite par rapport à laquelle on définit la symétrie ?

Si oui, il y a juste à calculer cet angle.

J'ai vu une matrice de rotation de cette forme-là :




Mais pas par rapport à une droite, mais je note-ça, et je vais essayer, ça réglerait mon souci je pense !

edith : j'avais pas vu l'ajout Merci !!

[Robic]

Si tu ne l'as pas vue pour les symétries, je te conseille plutôt l'autre méthode, qui est intuitive (on fait un dessin et on voit ce qu'il faut faire). En fait, je n'aime pas trop l'utilisation de formules toutes faites, ça n'aide pas à savoir ce qu'on fait...

(Ah oui, j'avais ajouté la 2ème méthode ensuite. En fait j'ai tapé le message tout en faisant l'exercice...)

[Subsib]

Si tu ne l'as pas vue pour les symétries, je te conseille plutôt l'autre méthode, qui est intuitive (on fait un dessin et on voit ce qu'il faut faire). En fait, je n'aime pas trop l'utilisation de formules toutes faites, ça n'aide pas à savoir ce qu'on fait...

(Ah oui, j'avais ajouté la 2ème méthode ensuite. En fait j'ai tapé le message tout en faisant l'exercice...)

Oui, je vois un peu mieux, mais je ne trouve toujours pas les calculs.

En fait, j'ai exprimé je ne sais pas combien de fois les vecteurs en fonction de (1,4) et (-4, 1), je trouve des choses intéressantes mais pas la matrice donnée en résultat.


me donne (1/17, 4/17)

Déjà, pour poser l'autre, je ne comprends pas. Si je fais avec les mêmes vecteurs sur (0,1):

me donne ... ben la même chose inversée, normal... :s (4/17, 1/17)

J'suis désolée, j'essaie hein, mais... là, je comprends vraiment pas.

[Robic]

Moi non plus, je ne comprends pas, c'est quoi ces lambda et mu ?

Je donne le début de la méthode exposée dans mon précédent message.

(1) Il faut calculer les coordonnées du vecteur (qui sont (x'-x,y'-y)...) puis exprimer que ce vecteur est perpendiculaire à la droite D. Comment exprime-t-on la perpendicularité quand on a des vecteurs ? Avec un produit scalaire. Si on choisit le vecteur u = (1,4) comme vecteur directeur de D, ça donnera : 1(x'-x) + 4(y'-y) = 0, c'est-à-dire x' + 4y' = x + 4y (j'ai mis les inconnues à gauche, comme d'habitude).

(2) Cette fois il faut calculer les coordonnées du vecteur . Je te laisse le faire. Ensuite il faut exprimer que ce vecteur est colinéaire à u(1,4). Le plus simple est de faire un produit en croix (pour n'avoir qu'une équation). Rappel : v(a,b) est colinéaire à v'(a',b') ssi ab' = a'b (c'est ça que j'appelle un produit en croix).

Etc.

[Sourire_banane]

Oui, je vois un peu mieux, mais je ne trouve toujours pas les calculs.

En fait, j'ai exprimé je ne sais pas combien de fois les vecteurs en fonction de (1,4) et (-4, 1), je trouve des choses intéressantes mais pas la matrice donnée en résultat.


me donne (1/17, 4/17)

Déjà, pour poser l'autre, je ne comprends pas. Si je fais avec les mêmes vecteurs sur (0,1):

me donne ... ben la même chose inversée, normal... :s (4/17, 1/17)

J'suis désolée, j'essaie hein, mais... là, je comprends vraiment pas.

Le pb, c'est que tu ne sais pas ce que tu fais.

Voyons cet exo d'un point de vue géométrique : La droite peut être paramétrée sous la forme Vect((1,4)).
Maintenant, tu dois trouver un vecteur e1' symétrique de e1 par rapport à la droite précédente, i.e qui soit de norme 1 (comme e1) et tel que e1+e1' appartienne à Vect((1,4)) soit encore "il existe a réel tel que (1,0)+(x,y)=(a,4a) avec e1'=(x,y)"
Alors une des précédentes conditions s'écrit x=a-1, y=4a et l'autre condition impose que sqrt(x²+y²)=1 soit 17a²-2a=0 soit encore successivement a=2/17 (attention, l'autre solution est a=0 mais elle ne sert à rien).
En remplaçant dans le système, on trouve que x=-15/17 et y=8/17.

Fais pareil avec e2, cela suffira.