Simplification d'arctan
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 20:08
par kokorico06 » 03 Nov 2011, 20:08
bonsoir, j'ai un exo où on me demande de simplifier arctan((1-x)/(1+x))
Je ne vois pas du tout quoi faire :s
Merci d'avance pour l'aide
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 20:16
par Skullkid » 03 Nov 2011, 20:16
Essaye de dériver, voir si tu obtiens un truc simple.
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 20:24
par kokorico06 » 03 Nov 2011, 20:24
Je trouve arctan'(...) = -1 / (x²+1)
Si encore je trouvais = 0 j'aurais fait le truc habituel pour trouver que c'est égal à une constante mais là je vois pas :/
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 20:26
par Skullkid » 03 Nov 2011, 20:26
Tu as donc montré que ta fonction est une primitive de -1/(x²+1) sur son domaine de dérivabilité (quel est-il, ce domaine ?). Quelles sont les primitives de x -> -1/(x²+1) ?
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 20:38
par kokorico06 » 03 Nov 2011, 20:38
Le domaine de dérivabilité est R.
Les primitives de -1/(x²+1) sont de la forme -arctan(x) + constante
Je vois tjrs pas où vous voulez en venir :/ (une vraie quiche)
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 20:42
par Skullkid » 03 Nov 2011, 20:42
kokorico06 a écrit:Le domaine de dérivabilité est R.
Non, regarde mieux.
kokorico a écrit:Les primitives de -1/(x²+1) sont de la forme -arctan(x) + constante
Je vois tjrs pas où vous voulez en venir :/ (une vraie quiche)
Si j'appelle f(x) = arctan((1-x)/(1+x)), tu as montré que f est une primitive de x -> -1/(x²+1) sur son domaine de dérivabilité, or les primitives de x -> -1/(x²+1) sont les K - arctan, donc...
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 20:48
par kokorico06 » 03 Nov 2011, 20:48
Je ne comprend pas. La dérivée de f(x) = arctan((1-x)/(1+x)) c'est bien -1/(x²+1) or x²+1 ne s'annule pas sur R donc le domaine de dérivabilité de f c'est bien R. Je ne comprend pas où ça doit nous mener :s
Peux tu me dire ce qu'on cherche à faire ?
Merci
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 20:52
par kokorico06 » 03 Nov 2011, 20:52
on a montré que arctan((1-x)/(1+x)) = -arctan(x) c'est bien ça ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 20:59
par Skullkid » 03 Nov 2011, 20:59
kokorico06 a écrit:Je ne comprend pas. La dérivée de f(x) = arctan((1-x)/(1+x)) c'est bien -1/(x²+1) or x²+1 ne s'annule pas sur R donc le domaine de dérivabilité de f c'est bien R.
Oui mais non. Un domaine de dérivabilité ça ne se trouve pas en calculant une dérivée à l'aveugle et en regardant a posteriori où l'expression qu'on obtient est définie. Le domaine de dérivabilité d'une fonction se calcule toujours a priori. Ici, ta fonction n'est même pas définie sur R tout entier, donc elle ne saurait être dérivable sur R.
kokorico06 a écrit:Je ne comprend pas où ça doit nous mener :s
Peux tu me dire ce qu'on cherche à faire ?
Merci
Je vois pas trop ce qui te bloque... f est une primitive de x -> -1/(x²+1) sur son domaine de dérivabilité, or les primitives de x -> -1/(x²+1) sont les K - arctan, donc f(x) est de la forme K - arctan(x) sur tout intervalle inclus dans son domaine de dérivabilité.
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:05
par kokorico06 » 03 Nov 2011, 21:05
D'accord donc le domaine de dérivabilité c'est alors R privé de -1.
donc la simplification de f c'est C - arctan(x) avec C une constante !
Dans la correction qu'ils nous donnent sur internet, la simplification donne Pi/4 - arctan(x) pour x> -1
et -3Pi/4 -arctan(x) pour x< -1. Comment on fait pour trouver ces deux nombres -Pi/4 et -3Pi/4 ???
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 21:12
par Skullkid » 03 Nov 2011, 21:12
Le domaine de dérivabilité de f est l'union de deux intervalles disjoints : ]-l'infini,-1[ et ]-1,+l'infini[, donc il existe deux constantes A et B telles que :
Pour tout x > -1 f(x) = A - arctan(x)
Pour tout x < -1 f(x) = B - arctan(x)
Pour trouver A et B il te suffit de regarder ce qui se passe pour certains x particuliers.
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:18
par kokorico06 » 03 Nov 2011, 21:18
Le seul x particulier que je vois ici c'est le -1, mais ça ne m'aide pas...
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:20
par kokorico06 » 03 Nov 2011, 21:20
Non c'est bon j'ai compris ! Je parle trop vite quelques fois ^^
Merci énormément pour ton aide =)
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:27
par kokorico06 » 03 Nov 2011, 21:27
Heu en fait pour les x>-1, j'ai pris x=0 ... et donc je trouve bien que ce que tu as appelé A = Pi/4
Mais pour les x<-1, je ne vois pas quel x choisir (y en a trop lol ^^), non sérieusement j'ai essayé avec x = -2 mais ça n'aboutit pas !
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 21:29
par Skullkid » 03 Nov 2011, 21:29
Ton idée de prendre x=-1 n'était pas idiote. Bien sûr f n'est pas définie en -1, mais tu peux regarder du côté des limites en -1.
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:35
par kokorico06 » 03 Nov 2011, 21:35
D'accord je me rapproche ! Pour la limite quand x tend vers -1 par valeurs supérieures je trouve A = Pi/4
et pour -1 par valeurs inférieures j'ai 3Pi/4
Tout petit problème, dans la correction c'est -3Pi/4 (et pas 3Pi/4) !
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:40
par kokorico06 » 03 Nov 2011, 21:40
Non non je rectifie pour -1 + ou -1 - j'obtiens la même constante qui est Pi/4
Le -3Pi/4 je n'ai aucune idée de comment le trouver
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 03 Nov 2011, 21:41
par Skullkid » 03 Nov 2011, 21:41
Quand x tend vers -1 par valeurs inférieures, (1-x)/(1+x) tend vers -l'infini, donc f(x) tend vers -pi/2. De l'autre côté, B - arctan(x) tend vers B + pi/4 donc B = -3pi/4. Tu peux aussi regarder ce qui se passe en -l'infini, tu tomberas aussi sur -3pi/4.
-
kokorico06
- Membre Relatif
- Messages: 130
- Enregistré le: 17 Oct 2011, 17:34
-
 par kokorico06 » 03 Nov 2011, 21:44
par kokorico06 » 03 Nov 2011, 21:44
Oh oui oui encore une fois stupide erreur de signe, j'avais oublié le - de -arctan(x)!
Pfff merci bien :)
J'arrête de t'embêter !
-
mathelot
 par mathelot » 03 Nov 2011, 21:58
par mathelot » 03 Nov 2011, 21:58
sinon, tu peux poser
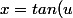)
avec
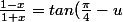)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
