busard_des_roseaux a écrit:On peut la dériver par rapport à x avec un coefficient multiplicatif
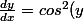)
(dérivée d'une fonction composée)
ou la dériver par rapport à la variable y avec un coefficient multiplicatif
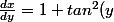)
à gauche. Ces deux coefficients sont inverses l'un de l'autre.
je veux simplement dire qu'avec y, les choses se simplifient mieux:
f(x) = Arctan(x) = y ; x =tan(y)
Soit à démontrer que :
f^(n)(x) = (n-1)! cos^(n)(y) sin(ny+ n;)/2) (I)
Pour n=1 la formule (I) sécrit : cosysin(y+

/2) =cos²y
Elle est donc vraie pour n=1
Supposons la vraie au rang n et dérivons la /y
On obtient : f^(n+1)(x)(1/cos²y))=
(n-1)![ncos^(n-1))(y)(-siny)sin(ny+ n;)/2)+n cos^(n)(y)cos(ny+n;)/2)]
Doù : f^(n+1)(x)=n!cos^(n+1)(y) [-siny sin(ny+ n;)/2)+cosy cos(ny+n;)/2)]
Et f(n+1)(x)=n!cos^(n+1)(y) cos((n+1)y+n;)/2) =
n!cos^(n+1)(y) sin((n+1)y+(n+1);)/2)
La formule (I) est donc montrée par récurrence
