Série de terme général n^µ(q^n)

[copinedeneo]

Bonjour,

j'ai un problème avec la question suivante:

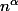
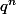
la série de terme général . avec un réel fixé > 0 converge ssi |q|< 1 .

N'ayant pas trouver de contre exemple j'ai supposé que c'était vrai , mais je ne sais pas comment le démontrer. Dois-je utiliser Riemann ? ou bien le critère des suites géométriques? Merci d'avance.

[fahr451]

vraie


si l ql >= 1 le terme général ne tend pas vers 0 la série diverge

si l q l < 1 on prend q ' avec

l ql < q ' < 1

et n^a l ql ^n = 0(q ' ^n) la série gémétrique de raison q ' converge donc l'autre aussi (absolument)

[copinedeneo]

:we: rerapide et refficace merci