Série de Fourier, bloque sur primitive

[Subsib]

Bonjour,

Je cherche à calculer dans les réels les séries de cette fonction :
f(x) = 0 pour -pi <= x <= 0
sin x pour 0 <= x <=pi

Bon, sur -pi, 0, ben ça vaut zéro, donc pas trop de calculs.
Maintenant, je continue sur 0 <= x <= pi

Je sais qu'il faut commencer par calculer et je trouve 2/pi.
Mais pour ça se gâte : il faut calculer
et je bloque sur l'intégrale :

heu... ?!
C'est bien ça qu'il faut faire, non ?

Je ne sais pas calculer cette intégrale, du coup, je suis coincée :/

Quelqu'un pourrait-il m'aider ?
Merci d'avance

[lionel52]

Salut

[Subsib]

Salut

ah oui, je vois, à partir de là, je manipule et je trouve...

a = t, b = 2t, tout simplement...

Je vais me mettre ça sur mon formulaire ^^

Merci beaucoup.

[paquito]

f n'étant ni paire, ni impaire, tu dois te payer tous les calculs:



On a: et c'est un cas évident de linéarisation, d'où



Je te laisse terminer; sinon plutôt que de stocker les formules trigonométriques sur une mémoire fragile, tu peux utiliser ta mémoire vive et utiliser un moyen mnémotechnique comme le:

coco sisi sico cosi;si ça t'intéresse....

[Subsib]

J'ai refait hier les calculs des 10aines de fois, et je ne trouvais jamais jusqu'à ce que je découvre que... je ne sais pas pourquoi, je considérais que nx = 2x... :mur:

Mais donc, j'ai fini par comprendre à peu près.

Si j'ose, j'ai du coup quelques questions :

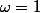
On a: et c'est un cas évident de linéarisation,

Je n'ai pas compris ni pour omega, ni pour le cas évident de linéarisation. (je préfère préciser que je suis une vieille qui a repris les études donc j'ai de grosses grosses lacunes, aussi les expressions consacrées, parfois, je ne les comprends pas )

sinon plutôt que de stocker les formules trigonométriques sur une mémoire fragile, tu peux utiliser ta mémoire vive et utiliser un moyen mnémotechnique comme le:

coco sisi sico cosi;si ça t'intéresse....

Oui, ça m'intéresse, je vais aller voir ça, d'autant que chaque fois qu'il y a de la trigo, j'ai le même souci ^^

Merci beaucoup de la suggestion

[mathelot]

Perso, je sais retrouver toutes les formules à partir
de
cos(a-b)=cos a cos b + sin a sin b (1)

(1) provient du produit scalaire de et

lire ici
rubrique Analyse: formules de trigo

[Ben314]

Perso (et il me semble bien que, si tu vois les séries de fourrier, ça devrait être la même chose pour toi), je sais inventer toute les formules de trigo. que tu veut en partant de .

[paquito]

cos(a+b)+cos(a-b)=2cos(a)cos(b)

cos(a+b)+cos(a-b)=-2sin(a)sin(b)

sin(a+b)+sin(a-b)=2sin(a)cos(b)

sin(a+b)-sin(a-b)=2cos(a)sin(b)

ça se mémorise très bien, en faisant gaffe qu'il y a un signe "-" à la 2ième ligne et en posant et , tu obtiens les formules de transformations de somme en produit.