Série de fonctions : convergence absolue mais non uniforme :
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 04 Nov 2012, 15:41
par Wenneguen » 04 Nov 2012, 15:41
Bonjour,
je dois donner un exemple de série de fonctions
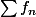
qui converge absolument sur

sans converger uniformément sur

, avec

un intervalle de

.
J'ai trouvé des exemples en cherchant une correction sur internet, mais plutôt que recopier bêtement l'un d'entre eux ( qui ne me paraissent pas très naturels ) j'aimerais réussir à en trouver un moi même, ce à quoi je ne parviens pas pour l'instant.
Quelqu'un pourrait-il m'aider à trouve une " méthode " pour trouver une telle série ?
Merci :we:

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 04 Nov 2012, 15:46
par raito123 » 04 Nov 2012, 15:46
Tu ne trouvera pas d'exemple parce qu'une série de fonctions qui converge absolument converge uniformément.
C'est plutôt l'inverse que tu dois chercher.
Les multiples ne doivent pas être utilisés sans nécessité
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 04 Nov 2012, 18:30
par Skullkid » 04 Nov 2012, 18:30
Bonjour, la convergence absolue de la série des f_n n'est jamais que la convergence simple de la série des |f_n|. En particulier, si tes fonctions sont positives, la convergence absolue équivaut à la convergence simple. Donc il te suffit de prendre un exemple de série de fonctions positives qui converge simplement mais non uniformément.
Si tu ne connais pas de tels exemples, la convergence simple (comme la convergence absolue) est une notion locale : on converge simplement en un point. En revanche, la convergence uniforme est une notion globale : on converge uniformément sur un ensemble de points, un intervalle le plus souvent. Une propriété à connaître est que lorsqu'une suite/série de fonctions continues sur A converge uniformément sur A, alors la fonction limite est elle-même continue sur A, mais ce n'est pas forcément le cas lorsqu'il n'y a que convergence simple. Donc une bonne piste à explorer c'est de chercher une série de fonctions continues et positives qui converge simplement vers une fonction non continue.
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 04 Nov 2012, 20:05
par Wenneguen » 04 Nov 2012, 20:05
Skullkid a écrit:Bonjour, la convergence absolue de la série des f_n n'est jamais que la convergence simple de la série des |f_n|. En particulier, si tes fonctions sont positives, la convergence absolue équivaut à la convergence simple. Donc il te suffit de prendre un exemple de série de fonctions positives qui converge simplement mais non uniformément.
Si tu ne connais pas de tels exemples, la convergence simple (comme la convergence absolue) est une notion locale : on converge simplement en un point. En revanche, la convergence uniforme est une notion globale : on converge uniformément sur un ensemble de points, un intervalle le plus souvent. Une propriété à connaître est que lorsqu'une suite/série de fonctions continues sur A converge uniformément sur A, alors la fonction limite est elle-même continue sur A, mais ce n'est pas forcément le cas lorsqu'il n'y a que convergence simple. Donc une bonne piste à explorer c'est de chercher une série de fonctions continues et positives qui converge simplement vers une fonction non continue.
D'accord merci, en effet ça me paraît être une démarche intelligente.
J'ai pensé à
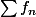
avec
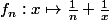
qui converge simplement vers
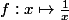
, qui n'est pas continue.
Malheureusement j'ai l'impression que la convergence est également uniforme :hum:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 04 Nov 2012, 20:22
par Skullkid » 04 Nov 2012, 20:22
Attention, d'une part tu as confondu suite et série (ce n'est pas très dur de passer de l'une à l'autre mais il faut quand même faire attention) et comme tu l'as dit, il y a convergence uniforme de la suite (mais pas de la série, qui diverge) des x -> 1/x + 1/n sur R*. Ces fonctions sont toutes continues sur R*, y compris la fonction inverse qui est la limite, ce n'est donc pas un bon exemple.
L'exemple typique de suite de fonctions simplement convergente mais non uniformément convergente c'est f_n(x) = x^n sur [0,1]. Montre que cette suite converge simplement sur ( = en tout point de) [0,1], mais qu'elle ne converge pas uniformément sur [0,1]. Ensuite, tu n'as plus qu'à trouver une série de fonctions qui se comporte comme la suite des x -> x^n.
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 04 Nov 2012, 20:46
par Wenneguen » 04 Nov 2012, 20:46
Skullkid a écrit:Attention, d'une part tu as confondu suite et série (ce n'est pas très dur de passer de l'une à l'autre mais il faut quand même faire attention) et comme tu l'as dit, il y a convergence uniforme de la suite (mais pas de la série, qui diverge) des x -> 1/x + 1/n sur R*. Ces fonctions sont toutes continues sur R*, y compris la fonction inverse qui est la limite, ce n'est donc pas un bon exemple.
L'exemple typique de suite de fonctions simplement convergente mais non uniformément convergente c'est f_n(x) = x^n sur [0,1]. Montre que cette suite converge simplement sur ( = en tout point de) [0,1], mais qu'elle ne converge pas uniformément sur [0,1]. Ensuite, tu n'as plus qu'à trouver une série de fonctions qui se comporte comme la suite des x -> x^n.
Merci je crois que j'ai réussi

J'avais vaguement pensé à ça mais j'avais laissé tombé l'idée à cause du fait qu'il fallait se restreindre à [0,1] alors que l'énoncé semble imposer un intervalle réel quelconque, mais je suppose que je peux passer outre ce détail :zen:
Edit : il faut d'ailleurs I = ]0,1[ plutôt, non ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 04 Nov 2012, 21:18
par Skullkid » 04 Nov 2012, 21:18
Wenneguen a écrit:Edit : il faut d'ailleurs I = ]0,1[ plutôt, non ?
Qu'est-ce qui te fait penser ça ? En l'occurrence ça ne change rien mais je trouve l'objection étonnante...
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
 par Wenneguen » 04 Nov 2012, 22:15
par Wenneguen » 04 Nov 2012, 22:15
Skullkid a écrit:Qu'est-ce qui te fait penser ça ? En l'occurrence ça ne change rien mais je trouve l'objection étonnante...
Ben pour x = 0,
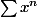
converge vers
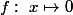
et pour x = 1 elle diverge, alors que pour x dans ]0,1[ , elle converge vers
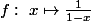
non ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 04 Nov 2012, 22:48
par Skullkid » 04 Nov 2012, 22:48
Ah ok, c'est parce que je parlais de la suite des x -> x^n et non pas de la série, le gras n'était sans doute pas suffisant...
Je voulais te faire parvenir à l'exemple de la série des x -> x^n - x^(n+1) sur [0,1] qui est en quelque sorte une série "sur" de la suite des x -> x^n. Cela dit ça marche aussi avec la série des x -> x^n sur ]0,1[ donc ton exemple est valide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
