Série entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 18 Mar 2024, 18:54
par ComeDuRondeau » 18 Mar 2024, 18:54
Bonjour,
Sait-on exprimer la série entière
!}x^n)
à l'aide des fonctions usuelles ?
En évaluant en

on peut voir que c'est équivalent à exprimer
}x^n)
mais je ne sais pas l'exprimer elle non plus.
Merci d'avance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2024, 19:41
par Ben314 » 18 Mar 2024, 19:41
Salut,
!}\ \mbox{ alors, pour }n\!\geqslant\!1\mbox{ on a }\ a_{n}=\dfrac{a_{n-1}}{2(2n-1)})
.
=\sum_{n\geqslant0}a_nx^n\ \mbox{ et qu'on pose }\ g(x)=x^{-1}\Big(f\big(x^2\big)-1\Big)=\sum_{n\geqslant1} a_n x^{2n-1}\ \mbox{ on a})
=\sum_{n\geqslant1}(2n\!-\!1)a_nx^{2n-2}=\frac{1}{2}\sum_{n\geqslant1}a_{n-1}x^{2n-2}=\frac{1}{2}\sum_{n\geqslant0}a_nx^{2n}=\frac{1}{2}+\frac{1}{2} x g(x))
Sait-tu résoudre cette équation différentielle ?
Modifié en dernier par
Ben314 le 18 Mar 2024, 20:29, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 18 Mar 2024, 20:03
par ComeDuRondeau » 18 Mar 2024, 20:03
Non, je ne sais pas la résoudre. En faisant une variation de la constante en posant
=\lambda(x)e^{x^4/4})
je tombe sur
=xe^{-x^4/4})
que je ne sais pas primitiver... Tu sais faire ?
En fait je suis tomber sur cette série justement en essayant de résoudre une équation différentielle haha. Il s'agit de
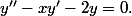
J'ai déjà trouvé
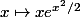
comme solution à l'aide de séries entières et je me demandais si je pouvais expliciter une autre solution pour avoir une base mais je n'y arrive pas.
Ça n'est pas très important de toute façon je n'ai besoin que de la première que j'ai déjà trouvé, la seconde c'était pour satisfaire ma curiosité !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2024, 20:34
par Ben314 » 18 Mar 2024, 20:34
Non, la primitive d'une telle fonction ne s'exprime pas à l'aide des fonctions vraiment usuelles, mais peut s'exprimer à l'aide de la "fonction d'erreur"
erf de Gauss (
https://fr.wikipedia.org/wiki/Fonction_d%27erreur) qui est relativement classique, surtout en proba/stat. vu que c'est (quasi) la fonction de répartition de la loi normale.
Sinon, j'ai modifié mon premier message vu que c'était pas la peine de rendre 4n-2 : 2n-1 suffisait largement.
Mais ça ne change rien concernant l'équation différentielle : elle est plus simple, mais on ne peut pas exprimer la solution sans "fonction spéciale" (en l’occurrence la fonction erf)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ComeDuRondeau
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Juil 2019, 12:59
-
 par ComeDuRondeau » 18 Mar 2024, 20:58
par ComeDuRondeau » 18 Mar 2024, 20:58
Ok, merci beaucoup pour tes réponses ! En voyant la tête de la série entière je me doutais un peu qu'on ne pourrait pas l'écrire à l'aide des fonctions usuelles mais en même temps je trouvais ça étonnant que pour une même équation différentielle on puisse exprimer certaines solutions à l'aide des fonctions usuelles et pas les autres !
Merci encore !!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2024, 21:02
par Ben314 » 18 Mar 2024, 21:02
Sinon, une fois que tu as une solution

de ton équation différentielle d'ordre 2, tu peut poser
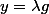
(où

est une fonction) et injecter ça dans l'équation : tu obtient une équation d'ordre 2 mais sans

donc d'ordre 1 en
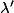
.
Et là, comme par hasard, tu retombe sur le même problème, à savoir que tu peut calculer
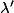
mais pas remonter à

sans utiliser la fonction d'erreur.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités