Semi-continuité faible inférieure

[melreg]

Bonjour!

Je cherche à savoir ce qu'est une fonction faiblement semi-continue inférieurement. J'ai cherché un peu et voilà ce que j'ai trouvé :

Définition
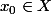
Soit X un espace topologique, , une fonction.
On dit que f est semi-continue inférieurement en si

Est-ce que mon intuition pour la définition suivante (je ne l'ai pas trouvé, c'est moi qui pense que cela doit ça!) est bonne?

Définition?
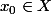
Soit X un espace topologique, , une fonction.
On dit que f est faiblement semi-continue inférieurement en si


Merci d'avance!

[Nightmare]

Re salut :happy3:

Je pense que ce n'est vrai que si on a l'équivalence entre la continuité séquentielle et la continuité, dans un métrique par exemple ou dans un espace topologique à base dénombrable.

[melreg]

Pour moi c'est donc un espace métrique... merci!
Mais sinon, par curiosité, tu connais la définition en toute généralité?

Re-merci

[melreg]

J'ai encore une question pour toi nightmare...

Comment montrer qu'une fonction continue, convexe est faiblement semi-continue inférieurement?

Pour éventuellement faciliter la preuve, la fonction est ...

[Nightmare]

Il me semble qu'une fonction est semi-continue inférieurement lorsque est ouvert pour tout x.

Pour ta propriété, je ne comprends pas vraiment puisqu'une fonction continue est toujours semi-continue (pas besoin de convexité)

[melreg]

Oui mais il y a le "faiblement"... J'aimerais voir que ma fonction J est faiblement semi-continue inférieurement et non pas "uniquement" semi-continue inférieurement...

Peut-être vas-tu me répondre qu'une fonction continue est faiblement continue?
Au fait, qu'est-ce qu'une fonction faiblement continue?

Enfin voici mon problème initial:

J'ai donc une fonction qui est convexe et continue. J'ai aussi une suite dans qui converge faiblement vers u dans . Alors, je dois montrer :

[Nightmare]

La continuité est liée aux ouverts donc à la topologie.

Une fonction est continue pour une topologie lorsque l'image réciproque de tout ouvert (de cette topologie) est ouverte (pour cette topologie).

Comme je l'ai dit, une fonction continue pour une topologie est semi-continue inférieurement et supérieurement pour cette topologie (c'est même une équivalence).

Quand ce n'est pas préciser, on dit qu'une fonction est continue lorsqu'elle l'est pour la topologie forte. Mais il n'est pas mauvais de rappeler que la topologie faible est plus faible que la topologie forte et donc une fonction fortement continue est effectivement faiblement continue.

[melreg]

D'accord avec tout ça!

Et en ce qui concerne le problème mentionné dans mon avant-dernier post?