Bonjour
Pour une fois que quelqu'un demande de l'aide et fait des efforts!
Voici mes remarques:
1. D'abord effectivement le résultat c'est celui donné par LB2. ça te servira si tu reprends tes calculs.
2. C'est pas idiot ce que tu as fait mais ça peut s'améliorer. J'expliquerai après.
3. Si on reste sur ta façon de faire ça doit aboutir. Il faute reprendre à partir du moment où tu remplaces par
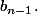
En effet ton expression de

est correcte donc pour avoir la bonne expression de b_{n-1}
il faut remplacer n par n-1
partout dans

(ce que tu n'a pas fait)
4. Concernant les simplifications

mérite d'être simplifié :
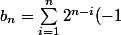^{i+1}=\sum_{j=0}^{n-1} 2^j (-1)^{n-j+1}=<br />(-1)^{n+1} \sum_{j=0}^{n-1} 2^j (-1)^j)
et on voit la somme des termes d'une suite géométrique de raison (-2) (i.e on utilise
=(q^n-1)/(q-1))
4. Concernant une simplifications encore: l'idée que tu exploites c'est qu'en regardant les premiers termes,
tu conjectures que

est de la forme
/c_n)
. A mon avis l'introduction de

est n peu inutile. Tu peux très bien entrer cela dans la

et le
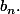
Autrement dit tu supposes que
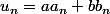
En faisant ça tu gardes malgré tout ton idée de base tout en simplifiant les calculs.