Résolution de système algébrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Moi12345
- Messages: 2
- Enregistré le: 23 Nov 2018, 17:28
-
par Moi12345 » 23 Nov 2018, 17:37
Bonjour,
Je suis en train de travailler sur un problème de mécanique et je bute sur la résolution du système ci-dessous. C'est probablement très simple mais je ne vois pas comment résoudre le système pour arriver au résultat proposé pour X et T1… Pourriez-vous m'expliquer cela s'il vous plaît?
Merci !
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 23 Nov 2018, 18:20
Salut,
- Soit tu as fait de l'algèbre linéaire et tu peut utiliser les formules de Cramer pour avoir directement le résultat.
- Soit tu as fait "légèrement" des résolutions de systèmes et tu peut fair un truc style algorithme du pivot de Gauss.
- Soit tu n'en a pas fait (ou tu as oublié) et tu fait comme on fait au collège, c'est à dire "par substitution" : tu utilise une des équation pour écrire (par exemple) X en fonction de T1 et tu reporte dans la deuxième pour n'avoir plus qu'une équation à une inconnue.
Ici, dans tout les cas la partie "logique du chmilblick" est totalement élémentaire, mais par contre, y'a besoin d'un peu connaître les formules de trigo. pour écrire simplement la solution du système (i.e sous la forme donnée sur ta photo)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
par Carpate » 23 Nov 2018, 18:42
Sauf erreur :
&\\ 0&sin(\theta-\frac{\alpha}{2}) <br />\end{array}<br />\right |}{\left| <br />\begin{array} {lr}<br />-sin(\theta-\alpha) & -cos(\theta-\frac{\alpha}{2})&\\ -cos(\theta-\alpha)&sin(\theta-\frac{\alpha}{2}) <br />\end{array}<br />\right |})
 & -m_1g&\\ -cos(\theta-\alpha)&0 <br />\end{array}<br />\right |}{\left| \begin{array} {lr}<br />-sin(\theta-\alpha) & -cos(\theta-\frac{\alpha}{2})&\\ -cos(\theta-\alpha)&sin(\theta-\frac{\alpha}{2}) <br />\end{array}<br />\right |})
Par exemple le dénominateur commun à
et
:
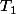
 & -cos(\theta-\frac{\alpha}{2})&\\ -cos(\theta-\alpha)&sin(\theta-\frac{\alpha}{2}) <br />\end{array}<br />\right |= -sin(\theta-\alpha)sin(\theta-\frac{\alpha}{2})+cos(\theta-\alpha)cos(\theta)-\frac{\alpha}{2})<br />=cos(\theta-\alpha-(\theta-\frac{\alpha}{2}))=cos(\frac{\alpha}{2}))
-
Moi12345
- Messages: 2
- Enregistré le: 23 Nov 2018, 17:28
-
par Moi12345 » 23 Nov 2018, 20:38
Merci beaucoup, je vais revoir tout ça !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
