Résolution de l'équation du 3ième degré

[Bouhachmoud]

Bonjour,comment faire résoudre cette équations de 3 éme degré ?

[Robot]

Il est bon de se souvenir que

(relations coefficients-racines)
Résoudre l'équation donnée, c'est donc trouver tel que

Le qui t'est rappelé (racine cubique de l'unité, qui vérifie 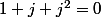), va bien sûr aider à exprimer les racines en fonction de et .

[Black Jack]

En se rappelant ce qui était jadis connu de tous : (A+B)³ = A³ + 3A²B + 3AB² + B³

3 AB.(A+B) = 3A²B + 3AB²

--> (A+B)³ - 3 AB.(A+B) = A³+B³

(-(A+B))³ - 3 AB.(-(A+B)) = - (A³+B³)

(-(A+B))³ - 3 AB.(-(A+B)) + (A³+B³) = 0

Et donc z = -(a+b) est solution de z³ - 3ab.z + a³+b³ = 0

--> P(z) = z³ - 3ab.z + a³+b³ est divisible par (z + a + b)

On fait la division euclidienne (sans difficulté), et on trouve :

z³ - 3ab.z + a³+b³ = (z + a + b)*(z² - (a+b).z + (a²+b²-ab))

Les solutions de z³ - 3ab.z + a³+b³ = 0 sont donc :

z1 = -(a+b)
et celles issues de la résolution de l'éq du second degré : z² - (a+b).z + (a²+b²-ab) = 0

soit donc : z = [(a+b) +/- (a²+b²+2ab - 4a²-4b²+4ab)^(1/2)]/2

z = [(a+b) +/- (-3a²-3b²+6ab)^(1/2)]/2
z = [(a+b) +/- V3 * (-a²-b²+2ab)^(1/2)]/2
z = (a+b)/2 +/- ((V3)/2) * i * (a-b)

Soit donc :
z1 = - (a+b)
z2 = (a+b)/2 - i.((V3)/2) * i * (a-b)
z3 = (a+b)/2 + i.((V3)/2) * i * (a-b)

Attention que (a+b) et (a-b) sont dans C

[aymanemaysae]

Bonjour,
Ma méthode est un peu similaire à celle de M.Black Jack (même beaucoup) .

On a les identités remarquables : et ,

donc



,

on a donc une solution , les deux autres solutions sont obtenues par la résolution de .

On a le discriminant ,

les deux autre solutions sont : et .

[Bouhachmoud]

Merci a vous

[Robot]

Puisque Black Jack et aymane ont fait l'exercice à la place du questionneur :
On factorise en produit de 3 facteurs, avec l'aide du qui est donné en indice ::

et on bricole (facile) pour que la somme des trois facteurs soit nulle :

Il ne reste plus, en posant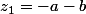 , , , qu'à vérifier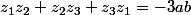
pour s'assurer qu'on a bien attrapé les trois racines.