Salut,
Pour la première question, la premier truc à dire, c'est déjà qu'on a pas grand chose à f.... de la réponse : les résidus, quand on les utilises, c'est pour ajouter tout ceux qui correspondent à des points situés dans un domaine donné et, quand tu fait une somme, s'il y a un/des zéros dedans, ils ne servent à rien donc ça n'a rien de gênant de dire "qu'ils n'existent pas".
Sinon, dans l'absolu, la réponse va bien évidement dépendre dépendre de la définition que tu prend de ce qu'est un résidu. Dans cette définition du "résidu de f en zo", si ça commence par "
Soit zo un pôle de f blablabla" alors cas ça n'a pas de sens de calculer un résidu en un point où tout les coeff. d'indice négatif de la série sont nuls vu qu'un tel point n'est pas un pôle de la fonction. Mais tu peut bien évidement écrire cette même définition sans imposer à zo d'être un pôle et dans ce cas le résidu existe et vaut 0.
Si on regarde par exemple la définition donné
sur wiki, on y voir un "
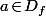
" avec "

isolé dans

ouvert" et "f holomorphe sur

\

" qui va plutôt dans le sens de dire qu'on ne calcule pas les résidus en n'importe quels point (encore que, rien ne dit que

ne contient pas des "fausses singularités" du style de
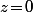
pour la fonction
}{z})
qui en fait n'est pas un pôle...). Enfin, bref, on en a rien à f... epicétout...
Et pour la deuxième question, je comprend pas vraiment où est le problème : tu as une fraction avec un numérteur et un dénominateur "super simples" donc il suffit de faire un D.L. des deux pour en déduire le début du développement en série de Laurent de la fraction et le seul truc, c'est qu'il faut être allé "suffisamment loin" dans les D.L. pour pouvoir évaluer la valeur du
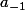
de la série de Laurent.
