Résidu

[barbu23]

Je ne comprends pas ce passage malheureusement. :mur:
Tu peux me l'expliquer ?
Pourquoi tu utilises le DL au voisinage de du sinus.
D'où vient cette formule : R = 1/2ipi * intégrale sur le cercle |z|=r de 2z - 4/3z + O(z^-3) dz ??? :mur:

[barbu23]

Pourquoi tu utilises le DL au voisinage de du sinus.
D'où vient cette formule : R = 1/2ipi * intégrale sur le cercle |z|=r de 2z - 4/3z + O(z^-3) dz ??? :mur:

[deltab]

Bonjour.

slayer191
on me demande de calculer le résidu de la fonction au point 1 qui est un point singulier essentiel. pourriez vous m'aider svp merci

Tu t'es bien basé sur quelque chose pour dire que z=1 est un point singulier essentiel.
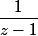
Quelles seront les puissances de qui vont apparaitre dans le développement en série de Laurent de , toutes ou uniquement les puissances impaires?

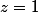
Remarque: Dire que existe contredit le fait que soit un point singulier essentiel.
Si la fonction sinus est bornée quand z est réel, elle ne l'est plus pour z complexe (Voir pou réel)

[Doraki]

Pourquoi tu utilises le DL au voisinage de du sinus.
D'où vient cette formule : R = 1/2ipi * intégrale sur le cercle |z|=r de 2z - 4/3z + O(z^-3) dz ??? :mur:

Parceque quand |z| est grand, 2/z tend vers 0 donc il faut bien que je fasse le DL de sin en 0 pour voir ce que fait sin(2/z) ???

Bonjour.
Tu t'es bien basé sur quelque chose pour dire que z=1 est un point singulier essentiel.

On a pas besoin de faire le développement en série de Laurent pour voir ça. Par exemple là, on voit tout de suite que z²sin(2/z) prend la valeur 0 une infinité de fois sur n'importe quel voisinage de z=0, donc il y a une singularité essentielle

[deltab]

Bonjour

Doraki
Parceque quand |z| est grand, 2/z tend vers 0 donc il faut bien que je fasse le DL de sin en 0 pour voir ce que fait sin(2/z) ???

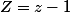
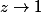
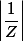
Mais ici tend vers 0 quand et donc tend vers l'infini quand

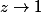
On a pas besoin de faire le développement en série de Laurent pour voir ça. Par exemple là, on voit tout de suite que z²sin(2/z) prend la valeur 0 une infinité de fois sur n'importe quel voisinage de z=0, donc il y a une singularité essentielle

Tu viens de répondre à ma question et la fonction nulle s'annule aussi une infinité de fois dans tout voisinage de 0, 0 est-il un point singulier essentiel pour la fonction nulle?

[Doraki]

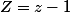
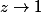
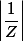
Mais ici tend vers 0 quand et donc tend vers l'infini quand

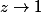
Personne ne t'a obligé à regarder ce qui se passe pour |Z| petit. N'importe quelle boucle qui tourne 1 fois autour de 0 dans le sens direct donne le résidu. Des fois on prend des boucles très petites. Si on regarde des boucles très petites on s'en sort pas pour calculer le résidu. Donc à la place on prend des boucles très grandes, et là le calcul est faisable.

Tu viens de répondre à ma question et la fonction nulle s'annule aussi une infinité de fois dans tout voisinage de 0, 0 est-il un point singulier essentiel pour la fonction nulle?

Ah ben oui j'aurais du rajouter que f est non identiquement nulle.